statistics --- 数字统计函数

Added in version 3.4.

源代码: Lib/statistics.py

---

该模块提供了用于计算数字 (Real-valued) 数据的数理统计量的函数。

此模块并不是诸如 NumPy, SciPy 等第三方库或者诸如 Minitab, SAS 和 Matlab 等针对专业统计学家的专有全功能统计软件包的竞品。 此模块针对图形和科学计算器的水平。

除非明确注释，这些函数支持 int ， float ， Decimal 和 Fraction 。当前不支持同其他类型（是否在数字塔中）的行为。混合类型的集合也是未定义的，并且依赖于实现。如果你输入的数据由混合类型组成，你应该能够使用 map() 来确保一个一致的结果，比如： map(float, input_data) 。

某些数据集合类型使用 NaN (not a number) 值来代表缺失的数据。 由于 NaN 具有特殊的比较语义，它们会在数据排序或计数等统计函数中产生怪异或未定义的行为。 受影响的函数有 median(), median_low(), median_high(), median_grouped(), mode(), multimode() 和 quantiles()。 NaN 值应当在调用这些函数之前被去除:

>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse

>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data)  # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data)  # This result is unexpected
16.35

>>> sum(map(isnan, data))    # Number of missing values
2
>>> clean = list(filterfalse(isnan, data))  # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean)  # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean)       # This result is now well defined
18.75

平均值以及对中心位置的评估

这些函数用于计算一个总体或样本的平均值或者典型值。

mean()	数据的算术平均数（“平均数”）。
fmean()	快速的浮点算术平均值，带有可选的权重设置。
geometric_mean()	数据的几何平均数
harmonic_mean()	数据的调和均值
kde()	估算数据的概率密度分布。
kde_random()	对由 kde() 生成的 PDF 进行随机采样。
median()	数据的中位数（中间值）
median_low()	数据的低中位数
median_high()	数据的高中位数
median_grouped()	分组数据的中位数（即第 50 个百分点的位置）。
mode()	离散的或标称的数据的单个众数（出现最多的值）。
multimode()	离散的或标称的数据的众数（出现最多的值）列表。
quantiles()	将数据以相等的概率分为多个间隔。

对分散程度的评估

这些函数用于计算总体或样本与典型值或平均值的偏离程度。

pstdev()	数据的总体标准差
pvariance()	数据的总体方差
stdev()	数据的样本标准差
variance()	数据的样本方差

对两个输入之间关系的统计

这些函数计算两个输入之间关系的统计值。

covariance()	两个变量的样本协方差。
correlation()	皮尔逊和斯皮尔曼相关系数。
linear_regression()	简单线性回归的斜率和截距。

函数细节

注释：这些函数不需要对提供给它们的数据进行排序。但是，为了方便阅读，大多数例子展示的是已排序的序列。

statistics.mean(data)

返回 data 的样本算术平均数，形式为序列或迭代器。

算术平均数是数据之和与数据点个数的商。通常称作“平均数”，尽管它指示诸多数学平均数之一。它是数据的中心位置的度量。

若 data 为空，将会引发 StatisticsError。

一些用法示例：

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

备注

平均数会受到 异常值 的强烈影响因而不一定能作为数据点的典型样本。 想获得对于 集中趋势 的更可靠的度量，可以参看 median()，但其效率要低一些。

样本均值给出了一个无偏向的真实总体均值的估计，因此当平均抽取所有可能的样本， mean(sample) 收敛于整个总体的真实均值。如果 data 代表整个总体而不是样本，那么 mean(data) 等同于计算真实整体均值 μ 。

statistics.fmean(data, weights=None)

将 data 转换成浮点数并且计算算术平均数。

此函数的运行速度比 mean() 函数快并且它总是返回一个 float。 data 可以为序列或可迭代对象。 如果输入数据集为空，则会引发 StatisticsError。

>>> fmean([3.5, 4.0, 5.25])
4.25

支持可选的权重参数。 例如，某位教授在为课程打分时可设置权重为测验 20%, 作业 20%, 期中考试 30%, 期末考试 30%:

>>> grades = [85, 92, 83, 91]
>>> weights = [0.20, 0.20, 0.30, 0.30]
>>> fmean(grades, weights)
87.6

如果提供了 weights，它必须与 data 的长度相同否则将引发 ValueError。

Added in version 3.8.

在 3.11 版本发生变更: 添加了对 weights 的支持。

statistics.geometric_mean(data)

将 data 转换成浮点数并且计算几何平均数。

几何平均值使用值的乘积表示 数据 的中心趋势或典型值（与使用它们的总和的算术平均值相反）。

如果输入数据集为空、包含零或包含负值则将引发 StatisticsError。 data 可以是序列或可迭代对象。

无需做出特殊努力即可获得准确的结果。（但是，将来或许会修改。）

>>> round(geometric_mean([54, 24, 36]), 1)
36.0

Added in version 3.8.

statistics.harmonic_mean(data, weights=None)

返回包含实数的序列或可迭代对象 data 的调和平均值。 如果 weights 被省略或为 None，则会假定为相等权重。

调和平均数是数据的倒数的算术平均值 mean() 的倒数。 例如，三个数值 a, b 和 c 的调和平均数将等于 3/(1/a + 1/b + 1/c)。 如果其中一个值为零，则结果也将为零。

调和平均数是均值的一种，是对数据的中心位置的度量。 它通常适用于求比率和比例（如速度）的均值。

假设一辆车在 40 km/hr 的速度下行驶了 10 km ，然后又以 60 km/hr 的速度行驶了 10 km 。车辆的平均速率是多少？

>>> harmonic_mean([40, 60])
48.0

假设一辆汽车以速度 40 公里/小时行驶了 5 公里，当道路变得畅通后，提速到 60 公里/小时行驶了行程中剩余的 30 km。 请问其平均速度是多少？

>>> harmonic_mean([40, 60], weights=[5, 30])
56.0

如果 data 为空、任意元素小于零，或者加权汇总值不为正数则会引发 StatisticsError。

当前算法在输入中遇到零时会提前退出。这意味着不会测试后续输入的有效性。（此行为将来可能会更改。）

Added in version 3.6.

在 3.10 版本发生变更: 添加了对 weights 的支持。

statistics.kde(data, h, kernel='normal', *, cumulative=False)

核密度估计 (KDE): 基于离散的样本创建一个连续概率密度函数或累积分布函数。

其基本思路是使用 核函数 来平滑数据。 以帮助根据一个样本来推断总体情况。

平滑等级是由被称为“带宽”的缩放形参 h 来控制的。 较小的值将强调局部特性而较大的值将给出更平滑的结果。

kernel 确定样本数据点的相对权重。 通常，对核形状的选择带来的影响没有对带宽平滑形参的选择那样大。

为每个样本点都给出一定权重的核包括 normal (gauss), logistic 和 sigmoid。

只为带宽范围内的样本点给出权重的核包括 rectangular (uniform), triangular, parabolic (epanechnikov), quartic (biweight), triweight 和 cosine。

如果 cumulative 为真值，将返回一个累积分布函数。

如果 data 序列为空则会引发 StatisticsError。

在 Wikipedia 提供的示例 中我们可以使用 kde() 来生成并绘制从小样本中估算出的概率密度函数：

>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> f_hat = kde(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [f_hat(x) for x in xarr]

xarr 和 yarr 中的点可被用来绘制一个 PDF 图形: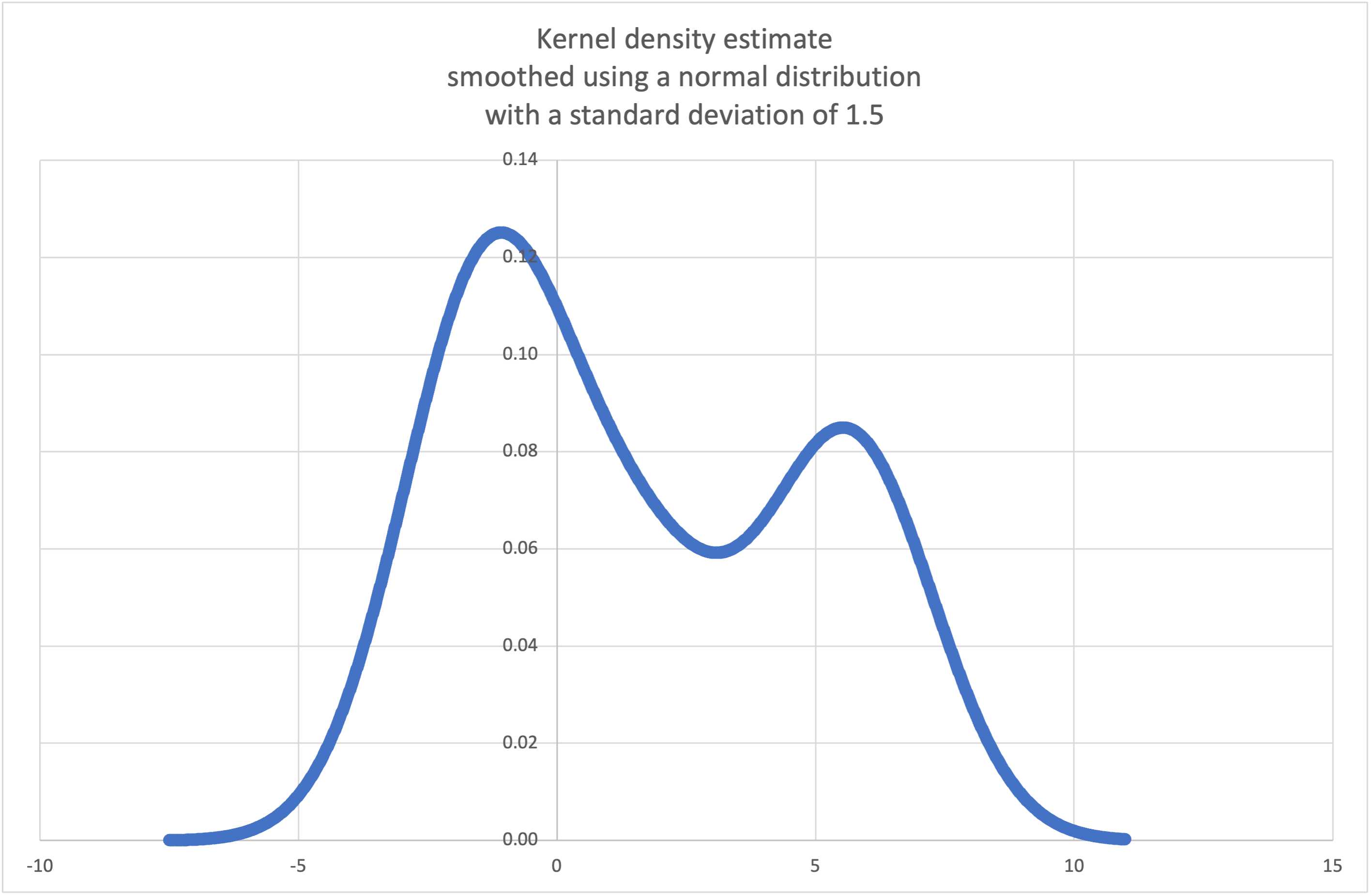

Added in version 3.13.

statistics.kde_random(data, h, kernel='normal', *, seed=None)

返回一个函数，从 kde(data, h, kernel) 产生的估计概率密度函数中执行一次随机选择。

提供 seed 将允许可重现的选择。 在未来版本中，这些值可能因更精确的反向 CDF 估计的实现而略微修改。 seed 可以是一个整数、浮点数、字符串或字节串。

如果 data 序列为空则会引发 StatisticsError。

继续 kde() 的例子，我们可以使用 kde_random() 从一个估计概率密度函数生成新的随机选择：

>>> data = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> rand = kde_random(data, h=1.5, seed=8675309)
>>> new_selections = [rand() for i in range(10)]
>>> [round(x, 1) for x in new_selections]
[0.7, 6.2, 1.2, 6.9, 7.0, 1.8, 2.5, -0.5, -1.8, 5.6]

Added in version 3.13.

statistics.median(data)

使用普通的“取中间两数平均值”方法返回数值数据的中位数（中间值）。 如果 data 为空，则将引发 StatisticsError。 data 可以是序列或可迭代对象。

中位数是衡量中间位置的可靠方式，并且较少受到极端值的影响。 当数据点的总数为奇数时，将返回中间数据点：

>>> median([1, 3, 5])
3

当数据点的总数为偶数时，中位数将通过对两个中间值求平均进行插值得出：

>>> median([1, 3, 5, 7])
4.0

这适用于当你的数据是离散的，并且你不介意中位数不是实际数据点的情况。

如果数据是有序的（支持排序操作）但不是数字（不支持加法），请考虑改用 median_low() 或 median_high()。

statistics.median_low(data)

返回数值数据的低中位数。 如果 data 为空则将引发 StatisticsError。 data 可以是序列或可迭代对象。

低中位数一定是数据集的成员。 当数据点总数为奇数时，将返回中间值。 当其为偶数时，将返回两个中间值中较小的那个。

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

当你的数据是离散的，并且你希望中位数是一个实际数据点而非插值结果时可以使用低中位数。

statistics.median_high(data)

返回数据的高中位数。 如果 data 为空则将引发 StatisticsError。 data 可以是序列或可迭代对象。

高中位数一定是数据集的成员。 当数据点总数为奇数时，将返回中间值。 当其为偶数时，将返回两个中间值中较大的那个。

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

当你的数据是离散的，并且你希望中位数是一个实际数据点而非插值结果时可以使用高中位数。

statistics.median_grouped(data, interval=1.0)

针对围绕连续的、固定宽度区间的中点进行了 分组或分档 的数值数据估算中位数。

data 可以是任意数值数据的可迭代对象，其中每个值都恰好为分档的中点。 至少必须有一个值。

interval 是每个分档的宽度。

例如，人口信息可能被归纳为按 10 年划分的连续年龄分组，每个分组由各区间的 5 年中点来表示：

>>> from collections import Counter
>>> demographics = Counter({
...    25: 172,   # 20 to 30 years old
...    35: 484,   # 30 to 40 years old
...    45: 387,   # 40 to 50 years old
...    55:  22,   # 50 to 60 years old
...    65:   6,   # 60 to 70 years old
... })
...

第 50 个百分点位置（中位数）就是 1071 名成员中的第 536 人。 此人属于 30 至 40 岁年龄分组。

常规的 median() 函数会假定三十至四十岁年龄组中的每个人都正好是 35 岁。 一个更站得住脚的假设则是该年龄组的 484 名成员均匀分布在 30 岁到 40 岁之间。 为此，我们会使用 median_grouped():

>>> data = list(demographics.elements())
>>> median(data)
35
>>> round(median_grouped(data, interval=10), 1)
37.5

调用者有责任确保数据点之间以 interval 的精确倍数分隔。 这对于获得正确结果至关重要。 该函数不会检查这一前提条件。

输入可以是任何可在插值步骤中强制转换为浮点数的数值类型。

statistics.mode(data)

从离散或标称的 data 返回单个出现最多的数据点。 此众数（如果存在）是最典型的值，并可用来度量中心的位置。

如果存在具有相同频率的多个众数，则返回在 data 中遇到的第一个。 如果想要其中最小或最大的一个，请使用 min(multimode(data)) 或 max(multimode(data))。 如果输入的 data 为空，则会引发 StatisticsError。

mode 将假定是离散数据并返回一个单一的值。 这是通常的学校教学中标准的处理方式：

>>> mode([1, 1, 2, 3, 3, 3, 3, 4])
3

此众数的独特之处在于它是这个包中唯一还可应用于标称（非数字）数据的统计信息：

>>> mode(["red", "blue", "blue", "red", "green", "red", "red"])
'red'

仅支持输入可哈希对象。 要处理 set 类型，可将其转换为 frozenset。 要处理 list 类型，可将其转换为 tuple。 对于混合的或嵌套的输入，可使用这个仅依赖于相等性检测的速度较慢的二次方复杂度算法: max(data, key=data.count)。

在 3.8 版本发生变更: 现在会通过返回所遇到的第一个众数来处理多模数据集。 之前它会在遇到超过一个的众数时引发 StatisticsError。

statistics.multimode(data)

返回最频繁出现的值的列表，并按它们在 data 中首次出现的位置排序。 如果存在多个众数则将返回一个以上的众数，或者如果 data 为空则将返回空列表：

>>> multimode('aabbbbccddddeeffffgg')
['b', 'd', 'f']
>>> multimode('')
[]

Added in version 3.8.

statistics.pstdev(data, mu=None)

返回总体标准差（总体方差的平方根）。 请参阅 pvariance() 了解参数和其他细节。

>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
0.986893273527251

statistics.pvariance(data, mu=None)

返回非空序列或包含实数值的可迭代对象 data 的总体方差。 方差或称相对于均值的二阶距，是对数据变化幅度（延展度或分散度）的度量。 方差值较大表明数据的散布范围较大；方差值较小表明它紧密聚集于均值附近。

如果给出了可选的第二个参数 mu，它应为 data 的 众数 均值。 它也可以被用来计算一个非均值点的二阶距。 如果该参数被省略或为 None (默认值)，则会自动进行算术均值计算。

使用此函数可根据所有数值来计算方差。 要根据一个样本来估算方差，通常 variance() 函数是更好的选择。

如果 data 为空则会引发 StatisticsError。

示例：

>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>> pvariance(data)
1.25

如果你已经计算过数据的平均值，你可以将其作为可选的第二个参数 mu 传入以避免重复计算：

>>> mu = mean(data)
>>> pvariance(data, mu)
1.25

同样也支持使用 Decimal 和 Fraction 值：

>>> from decimal import Decimal as D
>>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('24.815')

>>> from fractions import Fraction as F
>>> pvariance([F(1, 4), F(5, 4), F(1, 2)])
Fraction(13, 72)

备注

当调用时附带完整的总体数据时，这将给出总体方差 σ²。 而当调用时只附带一个样本时，这将给出偏置样本方差 s²，也被称为带有 N 个自由度的方差。

如果你通过某种方式知道了真实的总体平均值 μ，则可以使用此函数来计算一个样本的方差，并将已知的总体平均值作为第二个参数。 假设数据点是总体的一个随机样本，则结果将为总体方差的无偏估计值。

statistics.stdev(data, xbar=None)

返回样本标准差（样本方差的平方根）。 请参阅 variance() 了解参数和其他细节。

>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
1.0810874155219827

statistics.variance(data, xbar=None)

返回包含至少两个实数值的可迭代对象 data 的样本方差。 方差或称相对于均值的二阶矩，是对数据变化幅度（延展度或分散度）的度量。 方差值较大表明数据的散布范围较大；方差值较小表明它紧密聚集于均值附近。

如果给出了可选的第二个参数 xbar，它应为 data 的 样本 均值。 如果该参数省略或为 None (默认值)，则会自动进行均值计算。

当你的数据是总体数据的样本时请使用此函数。 要根据整个总体数据来计算方差，请参见 pvariance()。

如果 data 包含的值少于两个则会引发 StatisticsError。

示例：

>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> variance(data)
1.3720238095238095

如果你已经计算过数据的平均值，你可以将其作为可选的第二个参数 xbar 传入以避免重复计算：

>>> m = mean(data)
>>> variance(data, m)
1.3720238095238095

此函数不会试图检查你所传入的 xbar 是否为真实的平均值。 使用任意值作为 xbar 可能导致无效或不可能的结果。

同样也支持使用 Decimal 和 Fraction 值：

>>> from decimal import Decimal as D
>>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('31.01875')

>>> from fractions import Fraction as F
>>> variance([F(1, 6), F(1, 2), F(5, 3)])
Fraction(67, 108)

备注

这是附带贝塞尔校正的样本方差 s²，也称为具有 N-1 自由度的方差。 假设数据点具有代表性（即为独立且均匀的分布），则结果应当是对总体方差的无偏估计。

如果你通过某种方式知道了真实的总体平均值 μ 则应当调用 pvariance() 函数并将该值作为 mu 形参传入以得到一个样本的方差。

statistics.quantiles(data, *, n=4, method='exclusive')

将 data 分隔为具有相等概率的 n 个连续区间。 返回分隔这些区间的 n - 1 个分隔点的列表。

将 n 设为 4 以使用四分位（默认值）。 将 n 设为 10 以使用十分位。 将 n 设为 100 以使用百分位，即给出 99 个分隔点来将 data 分隔为 100 个大小相等的组。 如果 n 小于 1 则将引发 StatisticsError。

data 可以是包含样本数据的任意可迭代对象。 为了获得有意义的结果，data 中数据点的数量应当大于 n。 如果连一个数据点都没有则会引发 StatisticsError。

分隔点是通过对两个最接近的数据点进行线性插值得到的。 例如，如果一个分隔点落在两个样本值 100 和 112 之间距离三分之一的位置，则分隔点的取值将为 104。

method 用于计算分位值，它会由于 data 是包含还是排除总体的最低和最高可能值而有所不同。

默认 method 是 “唯一的” 并且被用于在总体中数据采样这样可以有比样本中找到的更多的极端值。落在 m 个排序数据点的第 i-th 个以下的总体部分被计算为 i / (m + 1) 。给定九个样本值，方法排序它们并且分配一下的百分位： 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% 。

将 method 设为 "inclusive" 可用于描述总体数据或已明确知道包含有总体数据中最极端值的样本。 data 中的最小值会被作为第 0 个百分位而最大值会被作为第 100 个百分位。 总体数据里处于 m 个已排序数据点中 第 i 个 以下的部分会以 (i - 1) / (m - 1) 来计算。 给定 11 个样本值，该方法会对它们进行排序并赋予以下百分位: 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100%。

# Decile cut points for empirically sampled data
>>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
...         100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
...         106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
...         111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
...         103, 107, 101, 81, 109, 104]
>>> [round(q, 1) for q in quantiles(data, n=10)]
[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

Added in version 3.8.

在 3.13 版本发生变更: 对于只有单个数据点的输入不会再引发异常。 这允许分位点估计以每次一个样本点的方式建立并随着每个新数据点逐渐变得更为精细。

statistics.covariance(x, y, /)

返回两个输入 x 和 y 的样本协方差。 样本协方差是对两个输入的同步变化性的度量。

两个输入必须具有相同的长度（不少于两个元素），否则会引发 StatisticsError。

示例：

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> covariance(x, y)
0.75
>>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> covariance(x, z)
-7.5
>>> covariance(z, x)
-7.5

Added in version 3.10.

statistics.correlation(x, y, /, *, method='linear')

返回两个输入的 皮尔逊相关系数。 皮尔逊相关系数 r 的取值在 -1 到 +1 之间。 它衡量线性相关的强度和方向。

如果 method 为 "ranked"，则计算两个输入的 斯皮尔曼等级相关系数。 数据将被替换为等级。 同级的值将被平均因此相同的值将得到相同的等级。 结果系数衡量的是单调关系的强度。

斯皮尔曼相关系数适用于有序数据或不满足皮尔逊相关系数的线性比例要求的连续数据。

两个输入必须具有相同的长度（不少于两个元素），并且不必为常量，否则会引发 StatisticsError。

使用 开普勒行星运动定律 的示例:

>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and  Neptune
>>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190]    # days
>>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km

>>> # Show that a perfect monotonic relationship exists
>>> correlation(orbital_period, dist_from_sun, method='ranked')
1.0

>>> # Observe that a linear relationship is imperfect
>>> round(correlation(orbital_period, dist_from_sun), 4)
0.9882

>>> # Demonstrate Kepler's third law: There is a linear correlation
>>> # between the square of the orbital period and the cube of the
>>> # distance from the sun.
>>> period_squared = [p * p for p in orbital_period]
>>> dist_cubed = [d * d * d for d in dist_from_sun]
>>> round(correlation(period_squared, dist_cubed), 4)
1.0

Added in version 3.10.

在 3.12 版本发生变更: 增加了对斯皮尔曼等级相关系数的支持。

statistics.linear_regression(x, y, /, *, proportional=False)

返回使用普通最小二乘法估计得到的 简单线性回归 参数的斜率和截距。 简单纯属回归通过此线性函数来描述自变量 x 和因变量 y 之间的关系。

y = slope * x + intercept + noise

其中 slope 和 intercept 是估计得到的回归参数，而 noise 代表不可由线性回归解释的数据变异性（它等于因变量的预测值和实际值之间的差异）。

两个输入必须具有相同的长度（不少于两个元素），并且自变量 x 不可为常量；否则会引发 StatisticsError。

例如，我们可以使用 Monty Python 系列电影的发布日期 在假定出品方保持现有步调的情况下预测到 2019 年时产出的 Monty Python 电影的累计数量。

>>> year = [1971, 1975, 1979, 1982, 1983]
>>> films_total = [1, 2, 3, 4, 5]
>>> slope, intercept = linear_regression(year, films_total)
>>> round(slope * 2019 + intercept)
16

如果 proportional 为真值，则自变量 x 和因变量 y 将被视为成正比关系。 数据会被拟合到一条通过原点的直线上。 由于 intercept 将始终为 0.0，因此下层的线性函数会简化为:

y = slope * x + noise

继续 correlation() 的例子，我们来看看基于大行星的模型是否能很好地预测矮行星的轨道距离：

>>> model = linear_regression(period_squared, dist_cubed, proportional=True)
>>> slope = model.slope

>>> # Dwarf planets:   Pluto,  Eris,    Makemake, Haumea, Ceres
>>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680]  # days
>>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods]
>>> list(map(round, predicted_dist))
[5912, 10166, 6806, 6459, 414]

>>> [5_906, 10_152, 6_796, 6_450, 414]  # actual distance in million km
[5906, 10152, 6796, 6450, 414]

Added in version 3.10.

在 3.11 版本发生变更: 添加了对 proportional 的支持。

异常

只定义了一个异常：

exception statistics.StatisticsError

ValueError 的子类，表示统计相关的异常。

NormalDist 对象

NormalDist 工具可用于创建和操纵 随机变量 的正态分布。 这个类将数据度量值的平均值和标准差作为单一实体来处理。

正态分布的概念来自于 中央极限定理 并且在统计学中有广泛的应用。

class statistics.NormalDist(mu=0.0, sigma=1.0)

返回一个新的 NormalDist 对象，其中 mu 代表 算术平均值 而 sigma 代表 标准差。

若 sigma 为负数，将会引发 StatisticsError。

mean

一个只读特征属性，表示特定正态分布的 算术平均值。

median

一个只读特征属性，表示特定正态分布的 中位数。

mode

一个只读特征属性，表示特定正态分布的 众数。

stdev

一个只读特征属性，表示特定正态分布的 标准差。

variance

一个只读特征属性，表示特定正态分布的 方差。 等于标准差的平方。

classmethod from_samples(data)

传入使用 fmean() 和 stdev() 基于 data 估算出的 mu 和 sigma 形参创建一个正态分布实例。

data 可以是任何 iterable 并且应当包含能被转换为 float 类型的值。 如果 data 不包含至少两个元素，则会引发 StatisticsError，因为估算中心值至少需要一个点而估算分散度至少需要两个点。

samples(n, *, seed=None)

对于给定的平均值和标准差生成 n 个随机样本。 返回一个由 float 值组成的 list。

当给定 seed 时，创建一个新的底层随机数生成器实例。 这适用于创建可重现的结果，即使对于多线程上下文也有效。

在 3.13 版本发生变更.

切换为更快速的算法。 要重新产生来自之前版本的样本，请使用 random.seed() 和 random.gauss()。

pdf(x)

使用 概率密度函数 (pdf)，计算一个随机变量 X 趋向于给定值 x 的相对可能性。 在数学意义上，它是当 dx 趋向于零时比率 P(x <= X < x+dx) / dx 的极限。

相对可能性的计算方法是用一个狭窄区间内某个样本出现的概率除以区间的宽度（因此使用 "density" 一词）。 由于可能性是相对于其他点的，因此它的值可以大于 1.0。

cdf(x)

使用 累积分布函数 (cdf)，计算一个随机变量 X 小于等于 x 的概率。 在数学上，它表示为 P(X <= x)。

inv_cdf(p)

计算反射累积分布函数，也称为 分位数函数 或 百分点 函数。 在数学上，它表示为 x : P(X <= x) = p。

找出随机变量 X 的值 x 使得该变量小于等于该值的概率等于给定的概率 p。

overlap(other)

测量两个正态概率分布之间的一致性。 返回介于 0.0 和 1.0 之间的值，给出 两个概率密度函数的重叠区域。

quantiles(n=4)

将指定正态分布划分为 n 个相等概率的连续分隔区。 返回这些分隔区对应的 (n - 1) 个分隔点的列表。

将 n 设为 4 以使用四分位（默认值）。 将 n 设为 10 以使用十分位。将 n 设为 100 以使用百分位，即给出 99 个分隔点来将正态分布分隔为 100 个大小相等的组。

zscore(x)

计算 标准分 即以高于或低于正态分布的平均值的标准差数值的形式来描述 x: (x - mean) / stdev.

Added in version 3.9.

NormalDist 的实例支持加上、减去、乘以或除以一个常量。 这些运算被用于转换和缩放。 例如：

>>> temperature_february = NormalDist(5, 2.5)             # Celsius
>>> temperature_february * (9/5) + 32                     # Fahrenheit
NormalDist(mu=41.0, sigma=4.5)

不允许一个常量除以 NormalDist 的实例，因为结果将不是正态分布。

由于正态分布是由独立变量的累加效应产生的，因此允许表示为 NormalDist 实例的 两组独立正态分布的随机变量相加和相减。 例如：

>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5])
>>> drug_effects = NormalDist(0.4, 0.15)
>>> combined = birth_weights + drug_effects
>>> round(combined.mean, 1)
3.1
>>> round(combined.stdev, 1)
0.5

Added in version 3.8.

例子和配方

经典概率问题

NormalDist 适合用来解决经典概率问题。

举例来说，如果 SAT 考试的历史数据 显示分数呈平均值为 1060 且标准差为 195 的正态分布，则可以确定考试分数处于 1100 和 1200 之间的学生的百分比舍入到最接近的整数应为：

>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4

求 SAT 分数的 四分位 和 十分位：

>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]

蒙特卡罗模拟输入

为了估算一个不易获得解析解的模型分布，NormalDist 可以生成用于 蒙特卡洛模拟 的输入样本：

>>> def model(x, y, z):
...     return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))       
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]

近似二项分布

当样本量较大且成功试验的可能性接近 50% 时，正态分布可以被用来模拟 二项式分布 。

例如，一次开源会议有 750 名与会者和两个可分别容纳 500 人的会议厅。 会上有一场关于 Python 的演讲和一场关于 Ruby 的演讲。 在往届会议中，65% 的与会者更愿意去听关于 Python 的演讲。 假定人群的偏好没有发生改变，那么 Python 演讲的会议厅不超出其容量上限的可能性是多少？

>>> n = 750             # Sample size
>>> p = 0.65            # Preference for Python
>>> q = 1.0 - p         # Preference for Ruby
>>> k = 500             # Room capacity

>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402

>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402

>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406

朴素贝叶斯分类器

在机器学习问题中也经常会出现正态分布。

维基百科上有一个 朴素贝叶斯分类器的良好样例。 要处理的问题是根据对多个分布的特征测量值包括身高、体重和足部尺码来预测一个人的性别。

我们得到了由八个人的测量值组成的训练数据集。 假定这些测量值是正态分布的，因此我们用 NormalDist 来总结数据：

>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])

接下来，我们遇到一个特征测量值已知但性别未知的新人：

>>> ht = 6.0        # height
>>> wt = 130        # weight
>>> fs = 8          # foot size

从是男是女各 50% 的 先验概率 出发，我们通过将该先验概率乘以给定性别的特征度量值的可能性累积值来计算后验概率：

>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
...                   weight_male.pdf(wt) * foot_size_male.pdf(fs))

>>> posterior_female = (prior_female * height_female.pdf(ht) *
...                     weight_female.pdf(wt) * foot_size_female.pdf(fs))

最终预测值应为最大后验概率值。 这种算法被称为 maximum a posteriori 或 MAP：

>>> 'male' if posterior_male > posterior_female else 'female'
'female'