statistics — Mathematical statistics functions

Added in version 3.4.

Вихідний код: Lib/statistics.py

---

Цей модуль надає функції для обчислення математичної статистики числових (Real-значних) даних.

The module is not intended to be a competitor to third-party libraries such as NumPy, SciPy, or proprietary full-featured statistics packages aimed at professional statisticians such as Minitab, SAS and Matlab. It is aimed at the level of graphing and scientific calculators.

Якщо не зазначено явно, ці функції підтримують int, float, Decimal і Fraction. Поведінка з іншими типами (у числовій вежі чи ні) наразі не підтримується. Колекції з сумішшю типів також не визначені та залежать від реалізації. Якщо ваші вхідні дані складаються зі змішаних типів, ви можете використовувати map(), щоб забезпечити послідовний результат, наприклад: map(float, input_data).

Some datasets use NaN (not a number) values to represent missing data. Since NaNs have unusual comparison semantics, they cause surprising or undefined behaviors in the statistics functions that sort data or that count occurrences. The functions affected are median(), median_low(), median_high(), median_grouped(), mode(), multimode(), and quantiles(). The NaN values should be stripped before calling these functions:

>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse

>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data)  # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data)  # This result is unexpected
16.35

>>> sum(map(isnan, data))    # Number of missing values
2
>>> clean = list(filterfalse(isnan, data))  # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean)  # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean)       # This result is now well defined
18.75

Середні значення та міри центрального розташування

Ці функції обчислюють середнє або типове значення з генеральної сукупності чи вибірки.

mean()	Середнє арифметичне («середнє») даних.
fmean()	Fast, floating-point arithmetic mean, with optional weighting.
геометричне_середнє()	Середнє геометричне даних.
harmonic_mean()	Середнє гармонійне даних.
kde()	Estimate the probability density distribution of the data.
kde_random()	Random sampling from the PDF generated by kde().
median()	Медіана (середнє значення) даних.
median_low()	Низька медіана даних.
median_high()	Висока медіана даних.
median_grouped()	Median (50th percentile) of grouped data.
mode()	Одиночний режим (найпоширеніше значення) дискретних або номінальних даних.
multimode()	Список режимів (найпоширеніших значень) дискретних або номінальних даних.
quantiles()	Розділіть дані на інтервали з рівною ймовірністю.

Міри поширення

Ці функції обчислюють міру того, наскільки генеральна сукупність або вибірка має тенденцію відхилятися від типових чи середніх значень.

pstdev()	Стандартне відхилення сукупності даних.
pvariance()	Популяційна дисперсія даних.
stdev()	Стандартне відхилення вибірки даних.
variance()	Вибіркова дисперсія даних.

Статистика для відносин між двома вхідними даними

Ці функції обчислюють статистичні дані щодо зв’язків між двома входами.

covariance()	Вибіркова коваріація для двох змінних.
correlation()	Pearson and Spearman’s correlation coefficients.
лінійна_регресія()	Нахил і відрізок для простої лінійної регресії.

Деталі функції

Примітка. Функції не вимагають сортування наданих їм даних. Однак для зручності читання більшість прикладів показують відсортовані послідовності.

statistics.mean(data)

Повертає зразкове середнє арифметичне даних, яке може бути послідовністю або ітерованим.

Середнє арифметичне — це сума даних, поділена на кількість точок даних. Його зазвичай називають «середнім», хоча це лише одне з багатьох різних математичних середніх. Це міра центрального розташування даних.

Якщо data порожній, буде викликано StatisticsError.

Деякі приклади використання:

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

Примітка

На середнє значення сильно впливають викиди і не обов’язково є типовим прикладом точок даних. Для більш надійного, хоча й менш ефективного вимірювання центральної тенденції, див. median().

Середнє значення вибірки дає неупереджену оцінку справжнього середнього значення генеральної сукупності, так що, узявши середнє значення за всіма можливими вибірками, «середнє (вибірка)» збігається зі справжнім середнім значенням усієї генеральної сукупності. Якщо data представляє всю генеральну сукупність, а не вибірку, тоді середнє (дані) еквівалентно обчисленню справжнього середнього µ генеральної сукупності.

statistics.fmean(data, weights=None)

Перетворіть дані на числа з плаваючою точкою та обчисліть середнє арифметичне.

Це працює швидше, ніж функція mean(), і завжди повертає float. Дані можуть бути послідовністю або ітерованими. Якщо вхідний набір даних порожній, виникає StatisticsError.

>>> fmean([3.5, 4.0, 5.25])
4.25

Optional weighting is supported. For example, a professor assigns a grade for a course by weighting quizzes at 20%, homework at 20%, a midterm exam at 30%, and a final exam at 30%:

>>> grades = [85, 92, 83, 91]
>>> weights = [0.20, 0.20, 0.30, 0.30]
>>> fmean(grades, weights)
87.6

If weights is supplied, it must be the same length as the data or a ValueError will be raised.

Added in version 3.8.

Змінено в версії 3.11: Додано підтримку ваги.

statistics.geometric_mean(data)

Перетворіть дані на числа з плаваючою точкою та обчисліть середнє геометричне.

Середнє геометричне вказує на центральну тенденцію або типове значення даних за допомогою добутку значень (на відміну від середнього арифметичного, яке використовує їх суму).

Викликає StatisticsError, якщо вхідний набір даних порожній, містить нуль або містить від’ємне значення. Дані можуть бути послідовністю або ітерованими.

Особливих зусиль для досягнення точних результатів не докладається. (Однак це може змінитися в майбутньому.)

>>> round(geometric_mean([54, 24, 36]), 1)
36.0

Added in version 3.8.

statistics.harmonic_mean(data, weights=None)

Return the harmonic mean of data, a sequence or iterable of real-valued numbers. If weights is omitted or None, then equal weighting is assumed.

Середнє гармонічне є зворотним арифметичним mean() зворотних величин даних. Наприклад, середнє гармонійне трьох значень a, b і c буде еквівалентним 3/(1/a + 1/b + 1/c). Якщо одне зі значень дорівнює нулю, результат буде нульовим.

Середнє гармонічне — це тип середнього значення, міра центрального розташування даних. Це часто доцільно під час усереднення співвідношень або швидкості, наприклад швидкості.

Припустимо, автомобіль проїжджає 10 км зі швидкістю 40 км/год, потім ще 10 км зі швидкістю 60 км/год. Яка середня швидкість?

>>> harmonic_mean([40, 60])
48.0

Припустімо, що автомобіль їде зі швидкістю 40 км/год протягом 5 км, а коли рух припиниться, розвиває швидкість до 60 км/год протягом решти 30 км шляху. Яка середня швидкість?

>>> harmonic_mean([40, 60], weights=[5, 30])
56.0

StatisticsError виникає, якщо data порожні, будь-який елемент менше нуля або якщо зважена сума не додатна.

Поточний алгоритм має ранній вихід, коли він зустрічає нуль у вхідних даних. Це означає, що наступні вхідні дані не перевіряються на дійсність. (Ця поведінка може змінитися в майбутньому.)

Added in version 3.6.

Змінено в версії 3.10: Додано підтримку ваги.

statistics.kde(data, h, kernel='normal', *, cumulative=False)

Kernel Density Estimation (KDE): Create a continuous probability density function or cumulative distribution function from discrete samples.

The basic idea is to smooth the data using a kernel function. to help draw inferences about a population from a sample.

The degree of smoothing is controlled by the scaling parameter h which is called the bandwidth. Smaller values emphasize local features while larger values give smoother results.

The kernel determines the relative weights of the sample data points. Generally, the choice of kernel shape does not matter as much as the more influential bandwidth smoothing parameter.

Kernels that give some weight to every sample point include normal (gauss), logistic, and sigmoid.

Kernels that only give weight to sample points within the bandwidth include rectangular (uniform), triangular, parabolic (epanechnikov), quartic (biweight), triweight, and cosine.

If cumulative is true, will return a cumulative distribution function.

A StatisticsError will be raised if the data sequence is empty.

Wikipedia has an example where we can use kde() to generate and plot a probability density function estimated from a small sample:

>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> f_hat = kde(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [f_hat(x) for x in xarr]

The points in xarr and yarr can be used to make a PDF plot: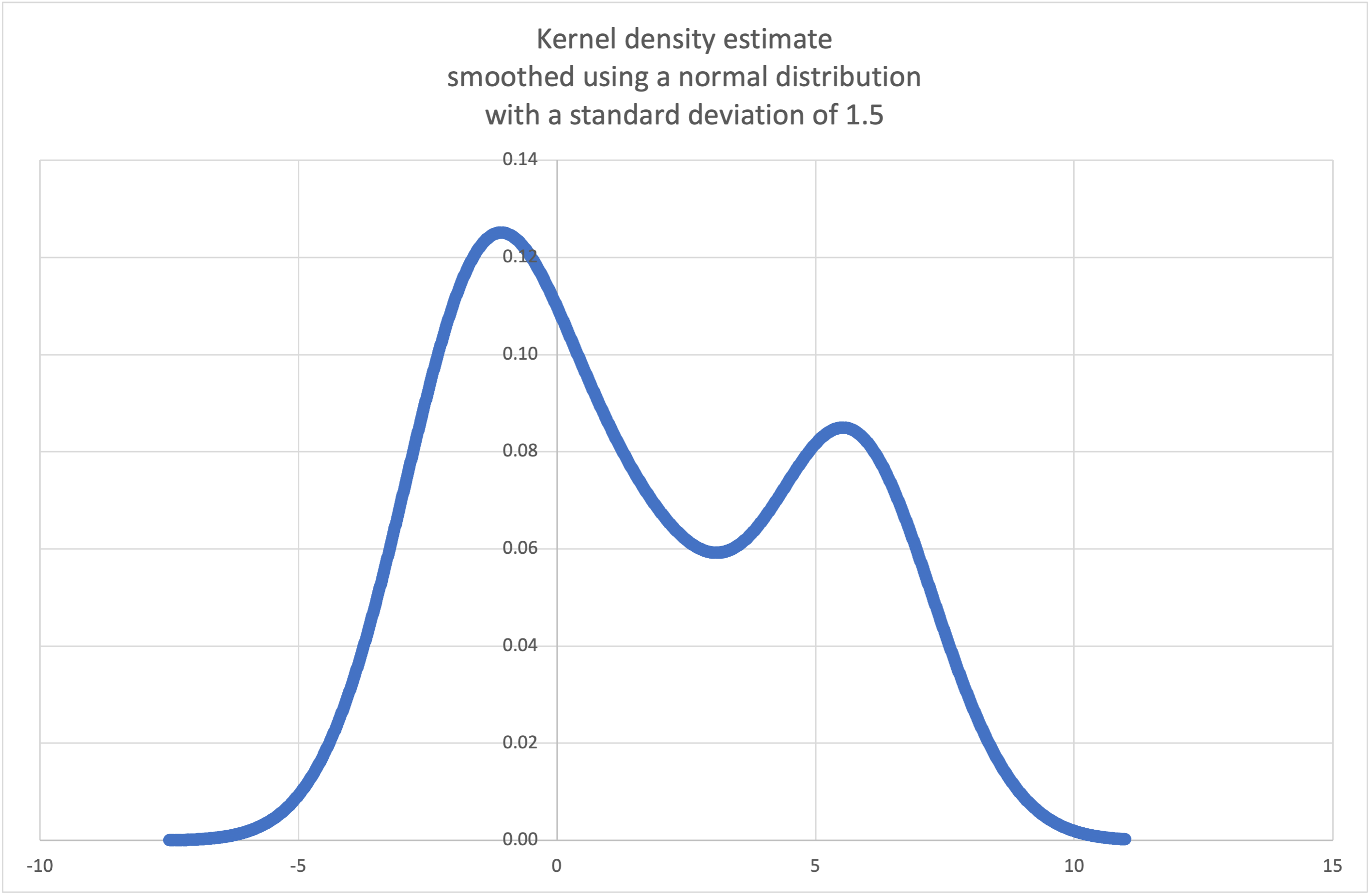

Added in version 3.13.

statistics.kde_random(data, h, kernel='normal', *, seed=None)

Return a function that makes a random selection from the estimated probability density function produced by kde(data, h, kernel).

Providing a seed allows reproducible selections. In the future, the values may change slightly as more accurate kernel inverse CDF estimates are implemented. The seed may be an integer, float, str, or bytes.

A StatisticsError will be raised if the data sequence is empty.

Continuing the example for kde(), we can use kde_random() to generate new random selections from an estimated probability density function:

>>> data = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> rand = kde_random(data, h=1.5, seed=8675309)
>>> new_selections = [rand() for i in range(10)]
>>> [round(x, 1) for x in new_selections]
[0.7, 6.2, 1.2, 6.9, 7.0, 1.8, 2.5, -0.5, -1.8, 5.6]

Added in version 3.13.

statistics.median(data)

Повертає медіану (середнє значення) числових даних, використовуючи поширений метод «середнього середнього двох». Якщо data порожній, виникає StatisticsError. data може бути послідовністю або ітерованою.

Медіана є надійним показником центрального розташування, і на неї менше впливає наявність викидів. Якщо кількість точок даних непарна, повертається середня точка даних:

>>> median([1, 3, 5])
3

Якщо кількість точок даних парна, медіана інтерполюється, беручи середнє значення двох середніх значень:

>>> median([1, 3, 5, 7])
4.0

Це підходить, коли ваші дані є дискретними, і ви не заперечуєте, що медіана може не бути фактичною точкою даних.

Якщо дані є порядковими (підтримують операції порядку), але не числовими (не підтримують додавання), подумайте про використання median_low() або median_high() натомість.

statistics.median_low(data)

Повертає нижню медіану числових даних. Якщо data порожній, виникає StatisticsError. data може бути послідовністю або ітерованою.

Нижня медіана завжди є членом набору даних. Якщо кількість точок даних непарна, повертається середнє значення. Якщо воно парне, повертається менше з двох середніх значень.

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

Використовуйте низьку медіану, якщо ваші дані є дискретними, і ви віддаєте перевагу, щоб медіана була фактичною точкою даних, а не інтерпольованою.

statistics.median_high(data)

Повернути високу медіану даних. Якщо data порожній, виникає StatisticsError. data може бути послідовністю або ітерованою.

Верхня медіана завжди є членом набору даних. Якщо кількість точок даних непарна, повертається середнє значення. Якщо воно парне, повертається більше з двох середніх значень.

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

Використовуйте високу медіану, якщо ваші дані є дискретними, і ви віддаєте перевагу, щоб медіана була фактичною точкою даних, а не інтерпольованою.

statistics.median_grouped(data, interval=1.0)

Estimates the median for numeric data that has been grouped or binned around the midpoints of consecutive, fixed-width intervals.

The data can be any iterable of numeric data with each value being exactly the midpoint of a bin. At least one value must be present.

The interval is the width of each bin.

For example, demographic information may have been summarized into consecutive ten-year age groups with each group being represented by the 5-year midpoints of the intervals:

>>> from collections import Counter
>>> demographics = Counter({
...    25: 172,   # 20 to 30 years old
...    35: 484,   # 30 to 40 years old
...    45: 387,   # 40 to 50 years old
...    55:  22,   # 50 to 60 years old
...    65:   6,   # 60 to 70 years old
... })
...

The 50th percentile (median) is the 536th person out of the 1071 member cohort. That person is in the 30 to 40 year old age group.

The regular median() function would assume that everyone in the tricenarian age group was exactly 35 years old. A more tenable assumption is that the 484 members of that age group are evenly distributed between 30 and 40. For that, we use median_grouped():

>>> data = list(demographics.elements())
>>> median(data)
35
>>> round(median_grouped(data, interval=10), 1)
37.5

The caller is responsible for making sure the data points are separated by exact multiples of interval. This is essential for getting a correct result. The function does not check this precondition.

Inputs may be any numeric type that can be coerced to a float during the interpolation step.

statistics.mode(data)

Повертає єдину найпоширенішу точку даних із дискретних або номінальних даних. Режим (якщо він існує) є найбільш типовим значенням і служить мірою центрального розташування.

Якщо є кілька режимів з однаковою частотою, повертає перший, який зустрічається в даних. Якщо натомість потрібне найменше або найбільше з них, використовуйте min(multimode(data)) або max(multimode(data)). Якщо введення data порожнє, виникає StatisticsError.

mode передбачає дискретні дані та повертає одне значення. Це стандартне лікування режиму, якому зазвичай навчають у школах:

>>> mode([1, 1, 2, 3, 3, 3, 3, 4])
3

Режим унікальний тим, що це єдина статистика в цьому пакеті, яка також застосовується до номінальних (нечислових) даних:

>>> mode(["red", "blue", "blue", "red", "green", "red", "red"])
'red'

Only hashable inputs are supported. To handle type set, consider casting to frozenset. To handle type list, consider casting to tuple. For mixed or nested inputs, consider using this slower quadratic algorithm that only depends on equality tests: max(data, key=data.count).

Змінено в версії 3.8: Тепер обробляє мультимодальні набори даних, повертаючи перший зустрічається режим. Раніше він викликав StatisticsError, коли було знайдено більше ніж один режим.

statistics.multimode(data)

Повертає список значень, які найчастіше зустрічаються, у тому порядку, в якому вони були вперше зустрінуті в даних. Поверне більше одного результату, якщо існує кілька режимів, або порожній список, якщо дані порожні:

>>> multimode('aabbbbccddddeeffffgg')
['b', 'd', 'f']
>>> multimode('')
[]

Added in version 3.8.

statistics.pstdev(data, mu=None)

Повертає стандартне відхилення сукупності (квадратний корінь із дисперсії сукупності). Перегляньте pvariance() для отримання аргументів та інших деталей.

>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
0.986893273527251

statistics.pvariance(data, mu=None)

Повертає дисперсію сукупності даних, непорожню послідовність або ітерацію дійсних чисел. Дисперсія, або другий момент відносно середнього, є мірою мінливості (розкиду або дисперсії) даних. Велика дисперсія вказує на те, що дані розкидані; невелика дисперсія вказує на те, що вона згрупована близько середнього значення.

If the optional second argument mu is given, it should be the population mean of the data. It can also be used to compute the second moment around a point that is not the mean. If it is missing or None (the default), the arithmetic mean is automatically calculated.

Використовуйте цю функцію, щоб обчислити дисперсію для всієї сукупності. Щоб оцінити дисперсію за вибіркою, функція variance() зазвичай є кращим вибором.

Викликає StatisticsError, якщо data порожні.

приклади:

>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>> pvariance(data)
1.25

Якщо ви вже обчислили середнє значення своїх даних, ви можете передати його як необов’язковий другий аргумент mu, щоб уникнути перерахунку:

>>> mu = mean(data)
>>> pvariance(data, mu)
1.25

Підтримуються десяткові знаки та дроби:

>>> from decimal import Decimal as D
>>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('24.815')

>>> from fractions import Fraction as F
>>> pvariance([F(1, 4), F(5, 4), F(1, 2)])
Fraction(13, 72)

Примітка

При виклику з усією сукупністю це дає дисперсію сукупності σ². Якщо замість цього викликати вибірку, це є дисперсія зміщеної вибірки s², також відома як дисперсія з N ступенями свободи.

Якщо ви якимось чином знаєте справжнє середнє значення сукупності μ, ви можете використати цю функцію для обчислення дисперсії вибірки, вказавши відоме середнє значення сукупності як другий аргумент. За умови, що точки даних є випадковою вибіркою сукупності, результатом буде неупереджена оцінка дисперсії генеральної сукупності.

statistics.stdev(data, xbar=None)

Повертає стандартне відхилення вибірки (квадратний корінь із дисперсії вибірки). Перегляньте variance() для отримання аргументів та інших деталей.

>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
1.0810874155219827

statistics.variance(data, xbar=None)

Повертає вибіркову дисперсію data, повторюваного принаймні двох дійсних чисел. Дисперсія, або другий момент відносно середнього, є мірою мінливості (розкиду або дисперсії) даних. Велика дисперсія вказує на те, що дані розкидані; невелика дисперсія вказує на те, що вона щільно згрупована навколо середнього значення.

If the optional second argument xbar is given, it should be the sample mean of data. If it is missing or None (the default), the mean is automatically calculated.

Використовуйте цю функцію, якщо ваші дані є вибіркою із генеральної сукупності. Щоб обчислити дисперсію для всієї сукупності, перегляньте pvariance().

Викликає StatisticsError, якщо data має менше двох значень.

приклади:

>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> variance(data)
1.3720238095238095

If you have already calculated the sample mean of your data, you can pass it as the optional second argument xbar to avoid recalculation:

>>> m = mean(data)
>>> variance(data, m)
1.3720238095238095

Ця функція не намагається перевірити, що ви передали фактичне середнє як xbar. Використання довільних значень для xbar може призвести до недійсних або неможливих результатів.

Підтримуються десяткові та дробові значення:

>>> from decimal import Decimal as D
>>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('31.01875')

>>> from fractions import Fraction as F
>>> variance([F(1, 6), F(1, 2), F(5, 3)])
Fraction(67, 108)

Примітка

Це вибіркова дисперсія s² з поправкою Бесселя, також відома як дисперсія з N-1 ступенями свободи. За умови, що точки даних є репрезентативними (наприклад, незалежними та однаково розподіленими), результат має бути неупередженою оцінкою справжньої дисперсії сукупності.

Якщо ви якимось чином знаєте фактичне середнє значення μ, ви повинні передати його функції pvariance() як параметр mu, щоб отримати дисперсію вибірки.

statistics.quantiles(data, *, n=4, method='exclusive')

Розділіть дані на n безперервних інтервалів з рівною ймовірністю. Повертає список n - 1 точок розрізу, що розділяють інтервали.

Встановіть n на 4 для квартилів (за замовчуванням). Встановіть n на 10 для децилів. Встановіть n на 100 для процентилів, що дає 99 точок розрізу, які розділяють дані на 100 груп однакового розміру. Викликає StatisticsError, якщо n не менше 1.

The data can be any iterable containing sample data. For meaningful results, the number of data points in data should be larger than n. Raises StatisticsError if there is not at least one data point.

Точки розрізу лінійно інтерполюються з двох найближчих точок даних. Наприклад, якщо точка зрізу падає на одну третину відстані між двома значеннями вибірки, 100 і 112, точка зрізу буде оцінена як 104.

Метод для обчислення квантилів може варіюватися залежно від того, чи дані включають чи виключають найнижчі та найвищі можливі значення з сукупності.

Метод за замовчуванням є «ексклюзивним» і використовується для даних, відібраних із сукупності, яка може мати більш екстремальні значення, ніж у вибірках. Частка генеральної сукупності, яка знаходиться нижче i-ї з m відсортованих точок даних, обчислюється як i / (m + 1). Маючи дев’ять значень вибірки, метод сортує їх і призначає наступні процентилі: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%.

Встановлення методу на «включно» використовується для опису даних сукупності або для вибірок, які, як відомо, включають найбільш екстремальні значення сукупності. Мінімальне значення в даних розглядається як 0-й процентиль, а максимальне значення розглядається як 100-й процентиль. Частка генеральної сукупності, що опускається нижче i-ї з m відсортованих точок даних, обчислюється як (i - 1) / (m - 1). Враховуючи 11 значень вибірки, метод сортує їх і призначає наступні процентилі: 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100%.

# Decile cut points for empirically sampled data
>>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
...         100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
...         106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
...         111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
...         103, 107, 101, 81, 109, 104]
>>> [round(q, 1) for q in quantiles(data, n=10)]
[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

Added in version 3.8.

Змінено в версії 3.13: No longer raises an exception for an input with only a single data point. This allows quantile estimates to be built up one sample point at a time becoming gradually more refined with each new data point.

statistics.covariance(x, y, /)

Повертає зразкову коваріацію двох вхідних даних x і y. Коваріація є мірою спільної мінливості двох вхідних даних.

Обидва входи мають бути однакової довжини (не менше двох), інакше виникає StatisticsError.

приклади:

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> covariance(x, y)
0.75
>>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> covariance(x, z)
-7.5
>>> covariance(z, x)
-7.5

Added in version 3.10.

statistics.correlation(x, y, /, *, method='linear')

Return the Pearson’s correlation coefficient for two inputs. Pearson’s correlation coefficient r takes values between -1 and +1. It measures the strength and direction of a linear relationship.

If method is «ranked», computes Spearman’s rank correlation coefficient for two inputs. The data is replaced by ranks. Ties are averaged so that equal values receive the same rank. The resulting coefficient measures the strength of a monotonic relationship.

Spearman’s correlation coefficient is appropriate for ordinal data or for continuous data that doesn’t meet the linear proportion requirement for Pearson’s correlation coefficient.

Обидва вхідні дані мають бути однакової довжини (не менше двох) і не повинні бути постійними, інакше виникає StatisticsError.

Example with Kepler’s laws of planetary motion:

>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and  Neptune
>>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190]    # days
>>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km

>>> # Show that a perfect monotonic relationship exists
>>> correlation(orbital_period, dist_from_sun, method='ranked')
1.0

>>> # Observe that a linear relationship is imperfect
>>> round(correlation(orbital_period, dist_from_sun), 4)
0.9882

>>> # Demonstrate Kepler's third law: There is a linear correlation
>>> # between the square of the orbital period and the cube of the
>>> # distance from the sun.
>>> period_squared = [p * p for p in orbital_period]
>>> dist_cubed = [d * d * d for d in dist_from_sun]
>>> round(correlation(period_squared, dist_cubed), 4)
1.0

Added in version 3.10.

Змінено в версії 3.12: Added support for Spearman’s rank correlation coefficient.

statistics.linear_regression(x, y, /, *, proportional=False)

Повертає нахил і відрізок параметрів простої лінійної регресії, оцінених за допомогою звичайних методів найменших квадратів. Проста лінійна регресія описує зв’язок між незалежною змінною x і залежною змінною y в термінах цієї лінійної функції:

y = нахил * x + перехоплення + шум

де нахил і перетин є параметрами регресії, які оцінюються, а шум представляє мінливість даних, яка не була пояснена лінійною регресією (він дорівнює різниці між прогнозованим і фактичні значення залежної змінної).

Обидва входи повинні мати однакову довжину (не менше двох), а незалежна змінна x не може бути постійною; інакше виникає StatisticsError.

Наприклад, ми можемо використати дати виходу фільмів Монті Пайтона, щоб передбачити загальну кількість фільмів Монті Пайтона, які були б створені до 2019 року, якщо припустити, що вони тримали темп.

>>> year = [1971, 1975, 1979, 1982, 1983]
>>> films_total = [1, 2, 3, 4, 5]
>>> slope, intercept = linear_regression(year, films_total)
>>> round(slope * 2019 + intercept)
16

If proportional is true, the independent variable x and the dependent variable y are assumed to be directly proportional. The data is fit to a line passing through the origin. Since the intercept will always be 0.0, the underlying linear function simplifies to:

y = slope * x + noise

Continuing the example from correlation(), we look to see how well a model based on major planets can predict the orbital distances for dwarf planets:

>>> model = linear_regression(period_squared, dist_cubed, proportional=True)
>>> slope = model.slope

>>> # Dwarf planets:   Pluto,  Eris,    Makemake, Haumea, Ceres
>>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680]  # days
>>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods]
>>> list(map(round, predicted_dist))
[5912, 10166, 6806, 6459, 414]

>>> [5_906, 10_152, 6_796, 6_450, 414]  # actual distance in million km
[5906, 10152, 6796, 6450, 414]

Added in version 3.10.

Змінено в версії 3.11: Added support for proportional.

Винятки

Визначено єдиний виняток:

exception statistics.StatisticsError

Підклас ValueError для винятків, пов’язаних зі статистикою.

NormalDist об’єкти

NormalDist — це інструмент для створення та керування нормальними розподілами випадкової змінної. Це клас, який розглядає середнє значення та стандартне відхилення вимірювань даних як єдине ціле.

Нормальні розподіли випливають із Центральної граничної теореми і мають широкий спектр застосувань у статистиці.

class statistics.NormalDist(mu=0.0, sigma=1.0)

Повертає новий об’єкт NormalDist, де mu представляє середнє арифметичне, а sigma являє собою стандартне відхилення.

Якщо сигма від’ємна, викликає StatisticsError.

mean

Властивість лише для читання для середнього арифметичного нормального розподілу.

median

Властивість лише для читання для медіани нормального розподілу.

mode

Властивість лише для читання для mode нормального розподілу.

stdev

Властивість лише для читання для стандартного відхилення нормального розподілу.

variance

Властивість лише для читання для variance нормального розподілу. Дорівнює квадрату стандартного відхилення.

classmethod from_samples(data)

Створює звичайний екземпляр розподілу з параметрами mu і sigma, оціненими з data за допомогою fmean() і stdev().

Data може бути будь-яким iterable і має складатися зі значень, які можна перетворити на тип float. Якщо data не містить принаймні двох елементів, виникає StatisticsError, оскільки для оцінки центрального значення потрібна принаймні одна точка, а для оцінки дисперсії — принаймні дві точки.

samples(n, *, seed=None)

Генерує n випадкових вибірок для заданого середнього значення та стандартного відхилення. Повертає list значень float.

Якщо задано seed, створюється новий екземпляр основного генератора випадкових чисел. Це корисно для створення відтворюваних результатів, навіть у багатопоточному контексті.

Змінено в версії 3.13.

Switched to a faster algorithm. To reproduce samples from previous versions, use random.seed() and random.gauss().

pdf(x)

Використовуючи функцію щільності ймовірності (pdf), обчисліть відносну ймовірність того, що випадкова змінна X буде близько заданого значення x. Математично, це межа відношення P(x <= X < x+dx) / dx, коли dx наближається до нуля.

The relative likelihood is computed as the probability of a sample occurring in a narrow range divided by the width of the range (hence the word «density»). Since the likelihood is relative to other points, its value can be greater than 1.0.

cdf(x)

Використовуючи кумулятивну функцію розподілу (cdf), обчисліть імовірність того, що випадкова змінна X буде меншою або дорівнює x. Математично це пишеться як P(X <= x).

inv_cdf(p)

Compute the inverse cumulative distribution function, also known as the quantile function or the percent-point function. Mathematically, it is written x : P(X <= x) = p.

Знаходить таке значення x випадкової змінної X, що ймовірність того, що змінна буде меншою або дорівнює цьому значенню, дорівнює заданій ймовірності p.

overlap(other)

Вимірює узгодженість між двома нормальними розподілами ймовірностей. Повертає значення від 0,0 до 1,0, що дає область перекриття для двох функцій щільності ймовірності.

quantiles(n=4)

Розділіть нормальний розподіл на n безперервних інтервалів з рівною ймовірністю. Повертає список (n - 1) точок розрізу, що розділяють інтервали.

Встановіть n на 4 для квартилів (за замовчуванням). Встановіть n на 10 для децилів. Встановіть n на 100 для процентилів, що дає 99 точок розсічення, які поділяють нормальний розподіл на 100 груп однакового розміру.

zscore(x)

Обчисліть Стандартну оцінку, що описує x у термінах кількості стандартних відхилень вище або нижче середнього нормального розподілу: (x - середнє) / стандартне відхилення.

Added in version 3.9.

Екземпляри NormalDist підтримують додавання, віднімання, множення та ділення на константу. Ці операції використовуються для перекладу та масштабування. Наприклад:

>>> temperature_february = NormalDist(5, 2.5)             # Celsius
>>> temperature_february * (9/5) + 32                     # Fahrenheit
NormalDist(mu=41.0, sigma=4.5)

Ділення константи на екземпляр NormalDist не підтримується, оскільки результат не розподілятиметься нормально.

Оскільки нормальний розподіл виникає внаслідок адитивних ефектів незалежних змінних, можна додавати та віднімати дві незалежні нормально розподілені випадкові змінні, представлені як екземпляри NormalDist. Наприклад:

>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5])
>>> drug_effects = NormalDist(0.4, 0.15)
>>> combined = birth_weights + drug_effects
>>> round(combined.mean, 1)
3.1
>>> round(combined.stdev, 1)
0.5

Added in version 3.8.

Приклади та рецепти

Classic probability problems

NormalDist легко вирішує класичні ймовірнісні проблеми.

Наприклад, враховуючи історичні дані для іспитів SAT, які показують, що бали зазвичай розподіляються із середнім значенням 1060 і стандартним відхиленням 195, визначте відсоток студентів із тестовими балами між 1100 і 1200 після округлення до найближчого цілого номер:

>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4

Знайдіть квартилі і децилі для результатів SAT:

>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]

Monte Carlo inputs for simulations

To estimate the distribution for a model that isn’t easy to solve analytically, NormalDist can generate input samples for a Monte Carlo simulation:

>>> def model(x, y, z):
...     return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))       
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]

Approximating binomial distributions

Normal distributions can be used to approximate Binomial distributions when the sample size is large and when the probability of a successful trial is near 50%.

Наприклад, конференція з відкритим кодом має 750 учасників і дві кімнати на 500 осіб. Є розмова про Python, а інша про Ruby. На попередніх конференціях 65% відвідувачів воліли слухати доповіді на Python. Якщо припустити, що переваги населення не змінилися, яка ймовірність того, що кімната Python залишиться в межах своїх можливостей?

>>> n = 750             # Sample size
>>> p = 0.65            # Preference for Python
>>> q = 1.0 - p         # Preference for Ruby
>>> k = 500             # Room capacity

>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402

>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402

>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406

Naive bayesian classifier

Нормальний розподіл зазвичай виникає в задачах машинного навчання.

Wikipedia has a nice example of a Naive Bayesian Classifier. The challenge is to predict a person’s gender from measurements of normally distributed features including height, weight, and foot size.

Нам надається навчальний набір даних із вимірюваннями для восьми осіб. Припускається, що вимірювання мають нормальний розподіл, тому ми підсумовуємо дані за допомогою NormalDist:

>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])

Далі ми зустрічаємо нову людину, характеристики якої відомі, але стать невідома:

>>> ht = 6.0        # height
>>> wt = 130        # weight
>>> fs = 8          # foot size

Починаючи з 50% попередньої ймовірності бути чоловіком чи жінкою, ми обчислюємо апостеріор як попередній час добуток ймовірностей для вимірювань ознаки з урахуванням статі:

>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
...                   weight_male.pdf(wt) * foot_size_male.pdf(fs))

>>> posterior_female = (prior_female * height_female.pdf(ht) *
...                     weight_female.pdf(wt) * foot_size_female.pdf(fs))

Остаточне передбачення йде до найбільшого заднього. Це відомо як maximum a posteriori або MAP:

>>> 'male' if posterior_male > posterior_female else 'female'
'female'