statistics — Funções estatísticas

Adicionado na versão 3.4.

Código-fonte: Lib/statistics.py

---

Esse módulo fornece funções para o cálculo de estatísticas matemáticas de dados numéricos (para valores do tipo Real).

O módulo não tem a intenção de competir com bibliotecas de terceiros como NumPy, SciPy, ou pacotes proprietários de estatísticas com todos os recursos destinados a estatísticos profissionais como Minitab, SAS e Matlab. Ela destina-se ao nível de calculadoras gráficas e científicas.

A menos que seja explicitamente indicado, essas funções suportam int, float, Decimal e Fraction. O uso com outros tipos (sejam numéricos ou não) não é atualmente suportado. Coleções com uma mistura de tipos também são indefinidas e dependentes da implementação. Se os seus dados de entrada consistem de tipos misturados, você pode usar map() para garantir um resultado consistente, por exemplo map(float, dado_entrada).

Alguns conjuntos de dados usam valores NaN (não um número) para representar dados ausentes. Como os NaNs possuem semântica de comparação incomum, eles causam comportamentos surpreendentes ou indefinidos nas funções estatísticas que classificam dados ou contam ocorrências. As funções afetadas são median(), median_low(), median_high(), median_grouped(), mode(), multimode() e quantiles(). Os valores NaN devem ser removidos antes de chamar estas funções:

>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse

>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data)  # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data)  # This result is unexpected
16.35

>>> sum(map(isnan, data))    # Number of missing values
2
>>> clean = list(filterfalse(isnan, data))  # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean)  # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean)       # This result is now well defined
18.75

Médias e medidas de valor central

Essas funções calculam a média ou o valor típico de uma população ou amostra.

mean()	Média aritmética dos dados.
fmean()	Média aritmética rápida de ponto flutuante, com ponderação opcional.
geometric_mean()	Média geométrica dos dados.
harmonic_mean()	Média harmônica dos dados.
median()	Mediana (valor do meio) dos dados.
median_low()	Mediana inferior dos dados.
median_high()	Mediana superior dos dados.
median_grouped()	Mediana (50º percentil) dos dados agrupados.
mode()	Moda (valor mais comum) de dados discretos ou nominais.
multimode()	Lista de modas (valores mais comuns) de dados discretos ou nominais.
quantiles()	Divide os dados em intervalos com probabilidade igual.

Medidas de espalhamento

Essas funções calculam o quanto a população ou amostra tendem a desviar dos valores típicos ou médios.

pstdev()	Desvio padrão populacional dos dados.
pvariance()	Variância populacional dos dados.
stdev()	Desvio padrão amostral dos dados.
variance()	Variância amostral dos dados.

Estatísticas para relações entre duas entradas

Essas funções calculam estatísticas sobre relações entre duas entradas.

covariance()	Covariância amostral para duas variáveis.
correlation()	Coeficientes de correlação de Pearson e Spearman.
linear_regression()	Inclinação e intersecção para regressão linear simples.

Detalhes das funções

Nota: as funções não exigem que os dados estejam ordenados. No entanto, para conveniência do leitor, a maioria dos exemplos mostrará sequências ordenadas.

statistics.mean(data)

Retorna a média aritmética amostral de data que pode ser uma sequência ou iterável.

A média aritmética é a soma dos dados dividida pela quantidade de dados. É comumente chamada apenas de “média”, apesar de ser uma das diversas médias matemáticas. Ela representa uma medida da localização central dos dados.

Se data for vazio, uma exceção do tipo StatisticsError será levantada.

Alguns exemplos de uso:

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

Nota

A média é fortemente afetada por outliers (valor atípico) e não é necessariamente um exemplo típico dos pontos de dados. Para uma medida mais robusta, embora menos eficiente, de tendência central, veja median().

A média amostral fornece uma estimativa não enviesada da média populacional verdadeira, ou seja, quando a média é obtida para todas as possíveis amostras, mean(sample) converge para a média verdadeira de toda população. Se data representa toda população ao invés de uma amostra, então mean(data) é equivalente a calcular a verdadeira média populacional μ.

statistics.fmean(data, weights=None)

Converte valores em data para ponto flutuante e calcula a média aritmética.

Essa função executa mais rapidamente do que a função mean() e sempre retorna um float. data pode ser uma sequência ou iterável. Se o conjunto de dados de entrada estiver vazio, levanta uma exceção StatisticsError.

>>> fmean([3.5, 4.0, 5.25])
4.25

A ponderação opcional é suportada. Por exemplo, um professor atribui uma nota para um curso ponderando questionários em 20%, trabalhos de casa em 20%, um exame de meio de período em 30% e um exame final em 30%:

>>> grades = [85, 92, 83, 91]
>>> weights = [0.20, 0.20, 0.30, 0.30]
>>> fmean(grades, weights)
87.6

Se weights for fornecido, deve ter o mesmo comprimento que data ou uma ValueError será levantada.

Adicionado na versão 3.8.

Alterado na versão 3.11: Adicionado suporte a weights.

statistics.geometric_mean(data)

Converte valores em data para ponto flutuante e calcula a média geométrica.

A média geométrica indica a tendência central ou valor típico de data usando o produto dos valores (em oposição à média aritmética que usa a soma deles).

Levanta uma exceção StatisticsError se a entrada do conjunto de dados for vazia, contiver um zero ou um valor negativo. data pode ser uma sequência ou iterável.

Nenhum esforço especial é feito para alcançar resultados exatos. (Mas, isso pode mudar no futuro).

>>> round(geometric_mean([54, 24, 36]), 1)
36.0

Adicionado na versão 3.8.

statistics.harmonic_mean(data, weights=None)

Retorna a média harmônica de data, uma sequência ou iterável de números de valor real. Se weights for omitido ou None, então a ponderação igual é presumida.

A média harmônica é a recíproca da média arimética calculada pela função mean() dos recíprocos dos dados. Por exemplo, a média harmônica de três valores a, b e c será equivalente a 3/(1/a + 1/b + 1/c). Se um dos valores for zero, o resultado também será zero.

A média harmônica é um tipo de média, uma medida de localização central dos dados. Ela é geralmente apropriada quando se está calculando a média de razões e taxas; por exemplo, velocidades.

Suponha que um carro viaje 10 km a 40 km/h, e em seguida viaje mais 10 km a 60 km/h. Qual é a velocidade média?

>>> harmonic_mean([40, 60])
48.0

Suponha que um carro viaja a 40 km/h por 5 km e, quando o trânsito melhora, acelera para 60 km/h pelos 30 km restantes da viagem. Qual é a velocidade média?

>>> harmonic_mean([40, 60], weights=[5, 30])
56.0

StatisticsError é levantada se data for vazio, qualquer elemento for menor que zero, ou se a soma ponderada não for positiva.

O algoritmo atual tem uma saída antecipada quando encontra um zero na entrada. Isso significa que as entradas subsequentes não tem a validade testada. (Esse comportamento pode mudar no futuro.)

Adicionado na versão 3.6.

Alterado na versão 3.10: Adicionado suporte a weights.

statistics.median(data)

Retorna a mediana (o valor do meio) de dados numéricos, usando o método comum de “média entre os dois do meio”. Se data for vazio, é levantada uma exceção StatisticsError. data pode ser uma sequência ou um iterável.

A mediana é uma medida robusta de localização central e é menos afetada por valores discrepantes. Quando a quantidade de pontos de dados for ímpar, o valor de meio é retornado:

>>> median([1, 3, 5])
3

Quando o número de elementos for par, a mediana é calculada tomando-se a média entre os dois valores no meio:

>>> median([1, 3, 5, 7])
4.0

Isso serve quando seus dados forem discretos e você não se importa que a média possa não ser um valor que de fato ocorre nos seus dados.

Caso os dados sejam ordinais (oferecem suporte para operações de ordenação) mas não são numéricos (não oferecem suporte para adição), considere usar a função median_low() ou median_high() no lugar.

statistics.median_low(data)

Retorna a mediana inferior de dados numéricos. Se data for vazio, a exceção StatisticsError é levantada. data pode ser uma sequência ou um iterável.

A mediana inferior sempre é um membro do conjunto de dados. Quando o número de elementos for ímpar, o valor intermediário é retornado. Se houver um número par de elementos, o menor entre os dois valores centrais é retornado.

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

Use a mediana inferior caso seus dados forem discretos e você prefira que a mediana seja um valor que de fato existe nos seus dados ao invés de um valor interpolado.

statistics.median_high(data)

Retorna a mediana superior de dados numéricos. Se data for vazio, a exceção StatisticsError é levantada. data pode ser uma sequência ou um iterável.

A mediana superior sempre é um membro do conjunto de dados. Quando o número de elementos for ímpar, o valor intermediário é retornado. Se houver um número par de elementos, o maior entre os dois valores centrais é retornado.

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

Use a mediana superior caso seus dados forem discretos e você prefira que a mediana seja um valor que de fato existe nos seus dados ao invés de um valor interpolado.

statistics.median_grouped(data, interval=1.0)

Estima a mediana para dados numéricos que foram agrupados ou “binned” em torno dos pontos médios de intervalos consecutivos de largura fixa.

The data can be any iterable of numeric data with each value being exactly the midpoint of a bin. At least one value must be present.

The interval is the width of each bin.

Por exemplo, as informações demográficas podem ter sido resumidas em grupos etários consecutivos de dez anos, com cada grupo sendo representado pelos pontos médios de cinco anos dos intervalos:

>>> from collections import Counter
>>> demographics = Counter({
...    25: 172,   # 20 to 30 years old
...    35: 484,   # 30 to 40 years old
...    45: 387,   # 40 to 50 years old
...    55:  22,   # 50 to 60 years old
...    65:   6,   # 60 to 70 years old
... })
...

O 50º percentil (mediana) é a 536ª pessoa de 1071 membros. Essa pessoa está na faixa etária de 30 a 40 anos.

A função regular median() iria presumir que todos na faixa etária tricenariana tinham exatamente 35 anos. Uma suposição mais sustentável é que os 484 membros dessa faixa etária estão distribuídos uniformemente entre 30 e 40. Para isso, usamos median_grouped():

>>> data = list(demographics.elements())
>>> median(data)
35
>>> round(median_grouped(data, interval=10), 1)
37.5

O chamador é responsável por garantir que os pontos de dados sejam separados por múltiplos exatos de intervalo. Isso é essencial para obter um resultado correto. A função não verifica essa pré-condição.

As entradas podem ser qualquer tipo numérico que possa ser convertido para um ponto flutuante durante a etapa de interpolação.

statistics.mode(data)

Retorna o valor mais comum dos dados discretos ou nominais em data. A moda (quando existe) é o valor mais típico e serve como uma medida de localização central.

Se existirem múltiplas modas com a mesma frequência, retorna a primeira encontrada em data. Se ao invés disso se desejar a menor ou a maior dentre elas, use min(multimode(data)) ou max(multimode(data)). Se a entrada data é vazia, a exceção StatisticsError é levantada.

mode presume que os dados são discretos e retorna um único valor. Esse é o tratamento padrão do conceito de moda normalmente ensinado nas escolas:

>>> mode([1, 1, 2, 3, 3, 3, 3, 4])
3

A moda é única no sentido que é a única medida estatística nesse módulo que também se aplica a dados nominais (não-numéricos):

>>> mode(["red", "blue", "blue", "red", "green", "red", "red"])
'red'

Somente entradas hasheáveis ​são suportadas. Para manipular o tipo set, considere fazer a conversão para frozenset. Para manipular o tipo list, considere fazer a conversão para tuple. Para entradas mistas ou aninhadas, considere usar este algoritmo quadrático mais lento que depende apenas de testes de igualdade: max(data, key=data.count).

Alterado na versão 3.8: Agora lida com conjunto de dados multimodais retornando a primeira moda encontrada. Anteriormente, ela levantava a exceção StatisticsError quando mais do que uma moda era encontrada.

statistics.multimode(data)

Retorna uma lista dos valores mais frequentes na ordem em que eles foram encontrados em data. Irá retornar mais do que um resultado se houver múltiplas modas ou uma lista vazia se data for vazio.

>>> multimode('aabbbbccddddeeffffgg')
['b', 'd', 'f']
>>> multimode('')
[]

Adicionado na versão 3.8.

statistics.pstdev(data, mu=None)

Retorna o desvio padrão populacional (a raiz quadrada da variância populacional). Veja os argumentos e outros detalhes em pvariance().

>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
0.986893273527251

statistics.pvariance(data, mu=None)

Retorna a variância populacional de data, que deve ser uma sequência ou iterável não-vazio de números reais. A variância, o segundo momento estatístico a partir da média, é uma medida da variabilidade (espalhamento ou dispersão) dos dados. Uma variância grande indica que os dados são espalhados; uma variância menor indica que os dados estão agrupado em volta da média.

Se o segundo argumento opcional mu for fornecido, ele deve ser a média da população dos dados em data. Ele também pode ser usado para calcular o segundo momento em torno de um ponto que não é a média. Se estiver faltando ou for None (o padrão), a média aritmética é calculada automaticamente.

Use essa função para calcular a variância de toda a população. Para estimar a variância de uma amostra, a função variance() costuma ser uma escolha melhor.

Levanta StatisticsError se data for vazio.

Exemplos:

>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>> pvariance(data)
1.25

Se você já calculou a média dos seus dados, você pode passar o valor no segundo argumento opcional mu para evitar recálculos:

>>> mu = mean(data)
>>> pvariance(data, mu)
1.25

Decimais e frações são suportadas:

>>> from decimal import Decimal as D
>>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('24.815')

>>> from fractions import Fraction as F
>>> pvariance([F(1, 4), F(5, 4), F(1, 2)])
Fraction(13, 72)

Nota

Quando os dados de entrada representarem toda a população, ele retorna a variância populacional σ². Se em vez disso, amostras forem usadas, então a variância amostral enviesada s², também conhecida como variância com N graus de liberdade é retornada.

Se de alguma forma você souber a verdadeira média populacional μ, você pode usar essa função para calcular a variância de uma amostra, fornecendo a média populacional conhecida como segundo argumento. Caso seja fornecido um conjunto de amostras aleatórias da população, o resultado será um estimador não enviesado da variância populacional.

statistics.stdev(data, xbar=None)

Retorna o desvio padrão amostral (a raiz quadrada da variância amostral). Veja variance() para argumentos e outros detalhes.

>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
1.0810874155219827

statistics.variance(data, xbar=None)

Retorna a variância amostral de data, que deve ser um iterável com pelo menos dois números reais. Variância, ou o segundo momento estatístico a partir da média, é uma medida de variabilidade (espalhamento ou dispersão) dos dados. Uma variância grande indica que os dados são espalhados, uma variância menor indica que os dados estão agrupados em volta da média.

If the optional second argument xbar is given, it should be the sample mean of data. If it is missing or None (the default), the mean is automatically calculated.

Use essa função quando seus dados representarem uma amostra da população. Para calcular a variância de toda população veja pvariance().

Levanta a exceção StatisticsError se data tiver menos do que dois valores.

Exemplos:

>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> variance(data)
1.3720238095238095

If you have already calculated the sample mean of your data, you can pass it as the optional second argument xbar to avoid recalculation:

>>> m = mean(data)
>>> variance(data, m)
1.3720238095238095

Essa função não verifica se você passou a média verdadeira como xbar. Usar valores arbitrários para xbar pode levar a resultados inválidos ou impossíveis.

Decimais e frações são suportados.

>>> from decimal import Decimal as D
>>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('31.01875')

>>> from fractions import Fraction as F
>>> variance([F(1, 6), F(1, 2), F(5, 3)])
Fraction(67, 108)

Nota

Essa é a variância amostral s² com a correção de Bessel, também conhecida como variância com N-1 graus de liberdade. Desde que os pontos de dados sejam representativos (por exemplo, independentes e distribuídos de forma idêntica), o resultado deve ser uma estimativa não enviesada da verdadeira variação populacional.

Caso você de alguma forma saiba a verdadeira média populacional μ você deveria passar para a função pvariance() como o parâmetro mu para obter a variância da amostra.

statistics.quantiles(data, *, n=4, method='exclusive')

Divide data em n intervalos contínuos com igual probabilidade. Retorna uma lista de n - 1 pontos de corte separando os intervalos.

Defina n como 4 para quartis (o padrão). Defina n como 10 para decis. Defina n como 100 para percentis, o que fornece os 99 pontos de corte que separam data em 100 grupos de tamanhos iguais. Levanta a exceção StatisticsError se n não for pelo menos 1.

data pode ser qualquer iterável contendo dados amostrais. Para resultados significativos, a quantidade de dados em data deve ser maior do que n. Levanta a exceção StatisticsError se não houver pelo menos dois pontos de dados.

Os pontos de corte são linearmente interpolados a partir dos dois pontos mais próximos. Por exemplo, se um ponto de corte cair em um terço da distância entre dois valores, 100 e 112, o ponto de corte será avaliado como 104.

O method para computar quantis pode variar dependendo se data incluir ou excluir os menores e maiores valores possíveis da população.

O valor padrão do parâmetro method é “exclusive” e é usado para dados amostrados de uma população que pode ter valores mais extremos do que os encontrados nas amostras. A porção da população que fica abaixo do i-ésimo item de m pontos ordenados é calculada como i / (m + 1). Dados nove valores, o método os ordena e atribui a eles os seguintes percentis: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%.

Definimos o parâmetro method para “inclusive” para descrever dados da população ou para amostras que são conhecidas por incluir os valores mais extremos da população. O mínimo valor em data é tratado como o percentil 0 e o máximo valor é tratado como percentil 100. A porção da população que fica abaixo do i-ésimo item de m pontos ordenados é calculada como (i - 1) / (m - 1). Dados 11 valores, o método os ordena e atribui a eles os seguintes percentis: 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100%.

# Decile cut points for empirically sampled data
>>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
...         100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
...         106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
...         111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
...         103, 107, 101, 81, 109, 104]
>>> [round(q, 1) for q in quantiles(data, n=10)]
[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

Adicionado na versão 3.8.

statistics.covariance(x, y, /)

Return the sample covariance of two inputs x and y. Covariance is a measure of the joint variability of two inputs.

Both inputs must be of the same length (no less than two), otherwise StatisticsError is raised.

Exemplos:

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> covariance(x, y)
0.75
>>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> covariance(x, z)
-7.5
>>> covariance(z, x)
-7.5

Adicionado na versão 3.10.

statistics.correlation(x, y, /, *, method='linear')

Return the Pearson’s correlation coefficient for two inputs. Pearson’s correlation coefficient r takes values between -1 and +1. It measures the strength and direction of a linear relationship.

If method is “ranked”, computes Spearman’s rank correlation coefficient for two inputs. The data is replaced by ranks. Ties are averaged so that equal values receive the same rank. The resulting coefficient measures the strength of a monotonic relationship.

Spearman’s correlation coefficient is appropriate for ordinal data or for continuous data that doesn’t meet the linear proportion requirement for Pearson’s correlation coefficient.

Both inputs must be of the same length (no less than two), and need not to be constant, otherwise StatisticsError is raised.

Example with Kepler’s laws of planetary motion:

>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and  Neptune
>>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190]    # days
>>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km

>>> # Show that a perfect monotonic relationship exists
>>> correlation(orbital_period, dist_from_sun, method='ranked')
1.0

>>> # Observe that a linear relationship is imperfect
>>> round(correlation(orbital_period, dist_from_sun), 4)
0.9882

>>> # Demonstrate Kepler's third law: There is a linear correlation
>>> # between the square of the orbital period and the cube of the
>>> # distance from the sun.
>>> period_squared = [p * p for p in orbital_period]
>>> dist_cubed = [d * d * d for d in dist_from_sun]
>>> round(correlation(period_squared, dist_cubed), 4)
1.0

Adicionado na versão 3.10.

Alterado na versão 3.12: Added support for Spearman’s rank correlation coefficient.

statistics.linear_regression(x, y, /, *, proportional=False)

Return the slope and intercept of simple linear regression parameters estimated using ordinary least squares. Simple linear regression describes the relationship between an independent variable x and a dependent variable y in terms of this linear function:

y = slope * x + intercept + noise

where slope and intercept are the regression parameters that are estimated, and noise represents the variability of the data that was not explained by the linear regression (it is equal to the difference between predicted and actual values of the dependent variable).

Both inputs must be of the same length (no less than two), and the independent variable x cannot be constant; otherwise a StatisticsError is raised.

For example, we can use the release dates of the Monty Python films to predict the cumulative number of Monty Python films that would have been produced by 2019 assuming that they had kept the pace.

>>> year = [1971, 1975, 1979, 1982, 1983]
>>> films_total = [1, 2, 3, 4, 5]
>>> slope, intercept = linear_regression(year, films_total)
>>> round(slope * 2019 + intercept)
16

If proportional is true, the independent variable x and the dependent variable y are assumed to be directly proportional. The data is fit to a line passing through the origin. Since the intercept will always be 0.0, the underlying linear function simplifies to:

y = slope * x + noise

Continuing the example from correlation(), we look to see how well a model based on major planets can predict the orbital distances for dwarf planets:

>>> model = linear_regression(period_squared, dist_cubed, proportional=True)
>>> slope = model.slope

>>> # Dwarf planets:   Pluto,  Eris,    Makemake, Haumea, Ceres
>>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680]  # days
>>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods]
>>> list(map(round, predicted_dist))
[5912, 10166, 6806, 6459, 414]

>>> [5_906, 10_152, 6_796, 6_450, 414]  # actual distance in million km
[5906, 10152, 6796, 6450, 414]

Adicionado na versão 3.10.

Alterado na versão 3.11: Added support for proportional.

Exceções

Uma única exceção é definida:

exception statistics.StatisticsError

Subclasse de ValueError para exceções relacionadas a estatísticas.

Objetos NormalDist

NormalDist é uma ferramenta para criar e manipular distribuições normais de uma variável aleatória. É uma classe que trata a média e o desvio padrão das medições de dados como uma entidade única.

Distribuições normais surgem do Teorema Central do Limite e possuem uma gama de aplicações em estatísticas.

class statistics.NormalDist(mu=0.0, sigma=1.0)

Retorna um novo objeto NormalDist onde mu representa a média aritmética e sigma representa o desvio padrão.

Se sigma for negativo, levanta a exceção StatisticsError.

mean

Uma propriedade somente leitura para a média aritmética de uma distribuição normal.

median

Uma propriedade somente leitura para a mediana de uma distribuição normal.

mode

Uma propriedade somente leitura para a moda de uma distribuição normal.

stdev

Uma propriedade somente leitura para o desvio padrão de uma distribuição normal.

variance

Uma propriedade somente leitura para a variância de uma distribuição normal. Igual ao quadrado do desvio padrão.

classmethod from_samples(data)

Faz uma instância da distribuição normal com os parâmetros mu e sigma estimados a partir de data usando fmean() e stdev().

data pode ser qualquer iterável e deve consistir de valores que pode ser convertidos para o tipo float. Se data não contém pelo menos dois elementos, levanta a exceção StatisticsError porque é preciso pelo menos um ponto para estimar um valor central e pelo menos dois pontos para estimar a dispersão.

samples(n, *, seed=None)

Gera n amostras aleatórias para uma dada média e desvio padrão. Retorna uma list de valores float.

Se o parâmetro seed for fornecido, cria uma nova instância do gerador de número aleatório subjacente. Isso é útil para criar resultados reproduzíveis, mesmo em um contexto multithreading.

pdf(x)

Usando uma função densidade de probabilidade (fdp), calcula a probabilidade relativa que uma variável aleatória X estará perto do valor dado x. Matematicamente, é o limite da razão P(x <= X < x+dx) / dx quando dx se aproxima de zero.

The relative likelihood is computed as the probability of a sample occurring in a narrow range divided by the width of the range (hence the word “density”). Since the likelihood is relative to other points, its value can be greater than 1.0.

cdf(x)

Usando uma função distribuição acumulada (fda), calcula a probabilidade de que uma variável aleatória X seja menor ou igual a x. Matematicamente, é representada da seguinte maneira: P(X <= x).

inv_cdf(p)

Calcula a função distribuição acumulada inversa, também conhecida como função quantil ou o função ponto percentual. Matematicamente, é representada como x : P(X <= x) = p.

Encontra o valor x da variável aleatória X de tal forma que a probabilidade da variável ser menor ou igual a esse valor seja igual à probabilidade dada p.

overlap(other)

Mede a concordância entre duas distribuições de probabilidade normais. Retorna um valor entre 0,0 e 1,0 fornecendo a área de sobreposição para as duas funções de densidade de probabilidade.

quantiles(n=4)

Divide a distribuição normal em n intervalos contínuos com probabilidade igual. Retorna uma lista de (n - 1) pontos de corte separando os intervalos.

Defina n como 4 para quartis (o padrão). Defina n como 10 para decis. Defina n como 100 para percentis, o que dá os 99 pontos de corte que separam a distribuição normal em 100 grupos de tamanhos iguais.

zscore(x)

Calcula a Pontuação Padrão (z-score) descrevendo x em termos do número de desvios padrão acima ou abaixo da média da distribuição normal: (x - mean) / stdev.

Adicionado na versão 3.9.

Instâncias de NormalDist suportam adição, subtração, multiplicação e divisão por uma constante. Essas operações são usadas para translação e dimensionamento. Por exemplo:

>>> temperature_february = NormalDist(5, 2.5)             # Celsius
>>> temperature_february * (9/5) + 32                     # Fahrenheit
NormalDist(mu=41.0, sigma=4.5)

A divisão de uma constante por uma instância de NormalDist não é suportada porque o resultado não seria distribuído normalmente.

Uma vez que distribuições normais surgem de efeitos aditivos de variáveis independentes, é possível adicionar e subtrair duas variáveis aleatórias independentes normalmente distribuídas representadas como instâncias de NormalDist. Por exemplo:

>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5])
>>> drug_effects = NormalDist(0.4, 0.15)
>>> combined = birth_weights + drug_effects
>>> round(combined.mean, 1)
3.1
>>> round(combined.stdev, 1)
0.5

Adicionado na versão 3.8.

Exemplos e receitas

Classic probability problems

NormalDist facilmente resolve problemas de probabilidade clássicos.

Por exemplo, considerando os dados históricos para exames SAT mostrando que as pontuações são normalmente distribuídas com média de 1060 e desvio padrão de 195, determine o percentual de alunos com pontuações de teste entre 1100 e 1200, após arredondar para o número inteiro mais próximo:

>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4

Encontrar os quartis e decis para as pontuações SAT:

>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]

Monte Carlo inputs for simulations

To estimate the distribution for a model that isn’t easy to solve analytically, NormalDist can generate input samples for a Monte Carlo simulation:

>>> def model(x, y, z):
...     return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))       
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]

Approximating binomial distributions

Normal distributions can be used to approximate Binomial distributions when the sample size is large and when the probability of a successful trial is near 50%.

Por exemplo, uma conferência de código aberto tem 750 participantes e duas salas com capacidade para 500 pessoas. Há uma palestra sobre Python e outra sobre Ruby. Em conferências anteriores, 65% dos participantes preferiram ouvir palestras sobre Python. Supondo que as preferências da população não tenham mudado, qual é a probabilidade da sala de Python permanecer dentro de seus limites de capacidade?

>>> n = 750             # Sample size
>>> p = 0.65            # Preference for Python
>>> q = 1.0 - p         # Preference for Ruby
>>> k = 500             # Room capacity

>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402

>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402

>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406

Naive bayesian classifier

Distribuições normais geralmente surgem em problemas de aprendizado de máquina.

Wikipedia has a nice example of a Naive Bayesian Classifier. The challenge is to predict a person’s gender from measurements of normally distributed features including height, weight, and foot size.

Recebemos um conjunto de dados de treinamento com medições para oito pessoas. As medidas são consideradas normalmente distribuídas, então resumimos os dados com NormalDist:

>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])

Em seguida, encontramos uma nova pessoa cujas características de medidas são conhecidas, mas cujo gênero é desconhecido:

>>> ht = 6.0        # height
>>> wt = 130        # weight
>>> fs = 8          # foot size

Começando com uma probabilidade a priori de 50% de ser homem ou mulher, calculamos a posteriori como a priori vezes o produto das probabilidade para as características de medidas dado o gênero:

>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
...                   weight_male.pdf(wt) * foot_size_male.pdf(fs))

>>> posterior_female = (prior_female * height_female.pdf(ht) *
...                     weight_female.pdf(wt) * foot_size_female.pdf(fs))

A previsão final vai para a probabilidade posterior maior. Isso é conhecido como máximo a posteriori ou MAP:

>>> 'male' if posterior_male > posterior_female else 'female'
'female'

Kernel density estimation

It is possible to estimate a continuous probability distribution from a fixed number of discrete samples.

The basic idea is to smooth the data using a kernel function such as a normal distribution, triangular distribution, or uniform distribution. The degree of smoothing is controlled by a scaling parameter, h, which is called the bandwidth.

from random import choice, random

def kde_normal(data, h):
    "Create a continuous probability distribution from discrete samples."

    # Smooth the data with a normal distribution kernel scaled by h.
    K_h = NormalDist(0.0, h)

    def pdf(x):
        'Probability density function.  P(x <= X < x+dx) / dx'
        return sum(K_h.pdf(x - x_i) for x_i in data) / len(data)

    def cdf(x):
        'Cumulative distribution function.  P(X <= x)'
        return sum(K_h.cdf(x - x_i) for x_i in data) / len(data)

    def rand():
        'Random selection from the probability distribution.'
        return choice(data) + K_h.inv_cdf(random())

    return pdf, cdf, rand

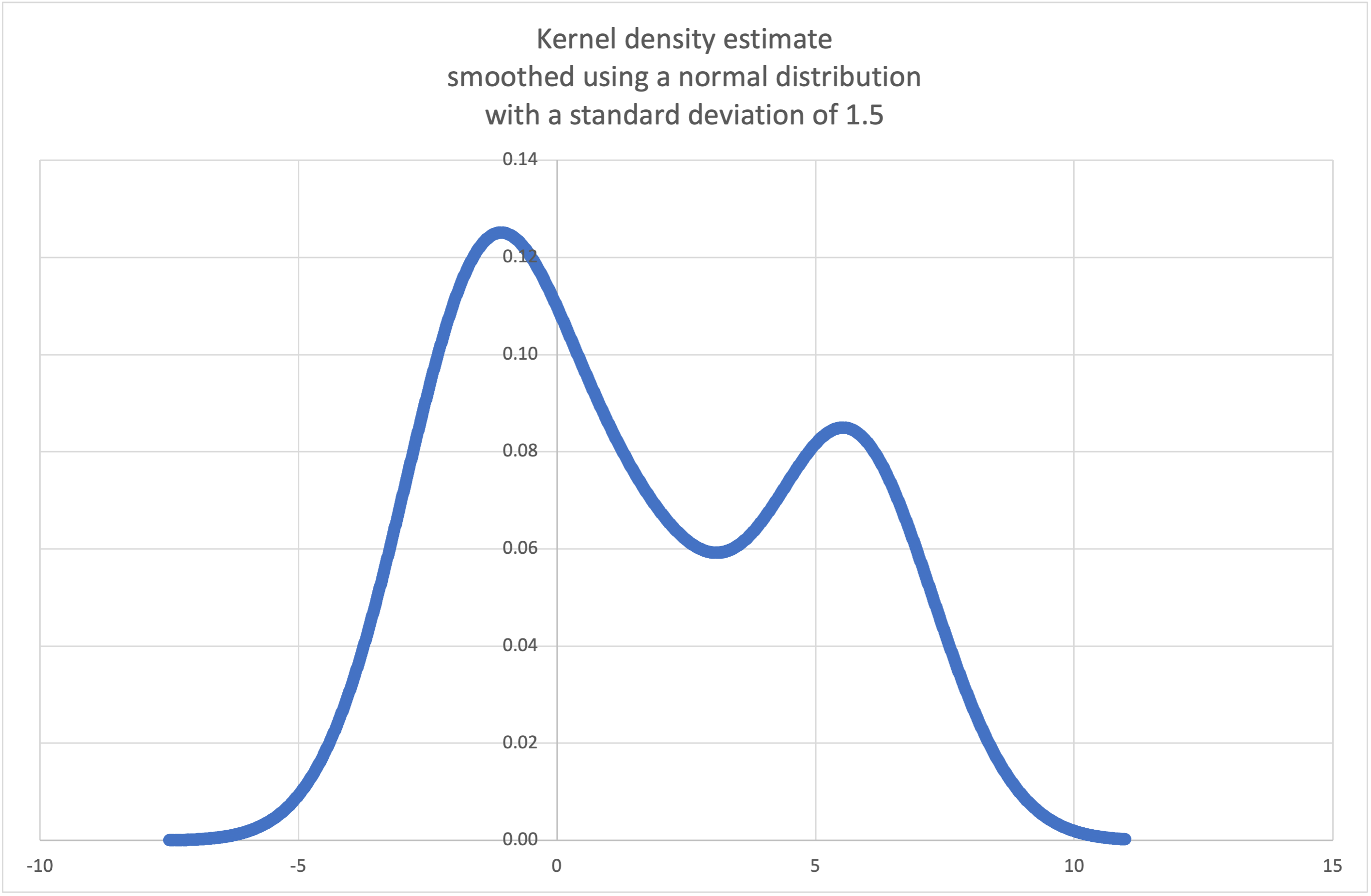
Wikipedia has an example where we can use the kde_normal() recipe to generate and plot a probability density function estimated from a small sample:

>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> pdf, cdf, rand = kde_normal(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [pdf(x) for x in xarr]

Os pontos em xarr e yarr podem ser usados ​para fazer um gráfico PDF:

Resample the data to produce 100 new selections:

>>> new_selections = [rand() for i in range(100)]

Determine the probability of a new selection being below 2.0:

>>> round(cdf(2.0), 4)
0.5794

Add a new sample data point and find the new CDF at 2.0:

>>> sample.append(4.9)
>>> round(cdf(2.0), 4)
0.5005