statistics --- 数学的統計関数¶
Added in version 3.4.
ソースコード: Lib/statistics.py
このモジュールは、数値 (Real 型) データを数学的に統計計算するための関数を提供します。
このモジュールは、 NumPy, SciPy のような third-party ライブラリや、Minitab、SAS、Matlab のようなプロ統計家向けのフル装備なプロプライエタリ統計パッケージと競合することを意図していません。グラフ関数電卓のレベルを対象としています。
特に明記しない限り、これらの関数は int, float, Decimal そして Fraction をサポートします。他の型 (算術型及びそれ以外) は現在サポートされていません。型が混ざったコレクションも未定義で実装依存です。入力データが複数の型からなる場合、map() を使用すると正しい結果が得られるでしょう。 例: map(float, input_data)。
あるデータセットでは欠損値を表すために NaN (not a number) を使います。 NaNは通常と異なる比較セマンティクスを持つため、ソートやカウントを行う統計関数では、驚きや未定義の振る舞いを引き起こします。 影響を受ける関数は median(), median_low(), median_high(), median_grouped(), mode(), multimode(), そして quantiles() です。 これらの関数を呼ぶ前に、 NaN 値を取り除く必要があります:
>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse
>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data) # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data) # This result is unexpected
16.35
>>> sum(map(isnan, data)) # Number of missing values
2
>>> clean = list(filterfalse(isnan, data)) # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean) # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean) # This result is now well defined
18.75
平均及び中心位置の測度¶
これらの関数は母集団または標本の平均値や標準値を計算します。
データの算術平均 (いわゆる「平均」) 。 |
|
Fast, floating-point arithmetic mean, with optional weighting. |
|
データの幾何平均。 |
|
データの調和平均。 |
|
データのメジアン(中央値)。 |
|
データの low median。 |
|
データの high median。 |
|
Median (50th percentile) of grouped data. |
|
離散/名義尺度データの最頻値 (single mode) 。 |
|
離散/名義尺度データの最頻値 (list of modes) 。 |
|
データの等確率での分割。 |
分散の測度¶
これらの関数は母集団または標本が標準値や平均値からどれくらい離れているかについて計算します。
データの母標準偏差。 |
|
データの母分散。 |
|
データの標本標準偏差。 |
|
データの標本標準分散。 |
2入力間の関係の統計¶
これらの関数は、2つの入力間の関係について統計量を計算します。
2変数の標本共分散。 |
|
ピアソンとスピアマンの相関係数。 |
|
単回帰の傾きと切片。 |
関数の詳細¶
註釈: 関数の引数となるデータをソートしておく必要はありません。例の多くがソートされているのは見やすさのためです。
- statistics.mean(data)¶
シーケンス型またはイテラブルになり得る data の標本算術平均を返します。
算術平均はデータの総和をデータ数で除したものです。単に「平均」と呼ばれることも多いですが、数学における平均の一種に過ぎません。データの中心位置の測度の一つです。
data が空の場合
StatisticsErrorを送出します。使用例:
>>> mean([1, 2, 3, 4, 4]) 2.8 >>> mean([-1.0, 2.5, 3.25, 5.75]) 2.625 >>> from fractions import Fraction as F >>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)]) Fraction(13, 21) >>> from decimal import Decimal as D >>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")]) Decimal('0.5625')
注釈
mean は 外れ値 (outliers) の影響を強く受け、必ずしもデータ点の典型例とはなりません。効率が悪いものの、より堅牢な、 中心的な傾向 (central tendency) の尺度については、
median()を参照してください。標本平均は真の母平均の不偏推定量のため、出来る限り多くの標本から平均を求めると、
mean(sample)は真の母平均に収束します (訳注: 大数の法則)。data が標本ではなく母集団全体の場合、mean(data)は真の母平均 μ を計算することと等価です。
- statistics.fmean(data, weights=None)¶
data を float に変換し、算術平均を計算します。
This runs faster than the
mean()function and it always returns afloat. The data may be a sequence or iterable. If the input dataset is empty, raises aStatisticsError.>>> fmean([3.5, 4.0, 5.25]) 4.25
Optional weighting is supported. For example, a professor assigns a grade for a course by weighting quizzes at 20%, homework at 20%, a midterm exam at 30%, and a final exam at 30%:
>>> grades = [85, 92, 83, 91] >>> weights = [0.20, 0.20, 0.30, 0.30] >>> fmean(grades, weights) 87.6
If weights is supplied, it must be the same length as the data or a
ValueErrorwill be raised.Added in version 3.8.
バージョン 3.11 で変更: weights のサポートが追加されました。
- statistics.geometric_mean(data)¶
Convert data to floats and compute the geometric mean.
The geometric mean indicates the central tendency or typical value of the data using the product of the values (as opposed to the arithmetic mean which uses their sum).
Raises a
StatisticsErrorif the input dataset is empty, if it contains a zero, or if it contains a negative value. The data may be a sequence or iterable.No special efforts are made to achieve exact results. (However, this may change in the future.)
>>> round(geometric_mean([54, 24, 36]), 1) 36.0
Added in version 3.8.
- statistics.harmonic_mean(data, weights=None)¶
Return the harmonic mean of data, a sequence or iterable of real-valued numbers. If weights is omitted or
None, then equal weighting is assumed.調和平均(harmonic mean)は、データの逆数の算術平均
mean()の逆数です。例えば、3つの値 a, b, c の調和平均は``3/(1/a + 1/b + 1/c)`` になります。いずれかの値が0の場合、結果は0になります。調和平均は平均の一種で、データの中心位置の測度です。速度のような比(ratios)や率(rates)を平均するときにしばしば適切です。
Suppose a car travels 10 km at 40 km/hr, then another 10 km at 60 km/hr. What is the average speed?
>>> harmonic_mean([40, 60]) 48.0
Suppose a car travels 40 km/hr for 5 km, and when traffic clears, speeds-up to 60 km/hr for the remaining 30 km of the journey. What is the average speed?
>>> harmonic_mean([40, 60], weights=[5, 30]) 56.0
StatisticsErroris raised if data is empty, any element is less than zero, or if the weighted sum isn't positive.The current algorithm has an early-out when it encounters a zero in the input. This means that the subsequent inputs are not tested for validity. (This behavior may change in the future.)
Added in version 3.6.
バージョン 3.10 で変更: weights のサポートが追加されました。
- statistics.median(data)¶
一般的な「中央2つの平均をとる」方法を使用して、数値データの中央値(中間値)を返します。もし data が空の場合、例外
StatisticsErrorが送出されます。data はシーケンス型またはイテラブルにもなれます。中央値は外れ値の影響を受けにくいため、中心位置のロバストな測度です。データ数が奇数の場合は中央の値を返します:
>>> median([1, 3, 5]) 3
データ数が偶数の場合は、中央値は中央に最も近い2値の算術平均で補間されます:
>>> median([1, 3, 5, 7]) 4.0
データが離散的で、中央値がデータ点にない値でも構わない場合に適しています。
もしあなたのデータが(注文操作をサポートする)序数で、(追加操作をサポートしない)数値でないならば、代わりに
median_low()またはmedian_high()の使用を検討してください。
- statistics.median_low(data)¶
数値データの小さい方の中央値(low median)を返します。もし data が空の場合、
StatisticsErrorが送出されます。data はシーケンス型またはイテラブルにもなれます。low median は必ずデータに含まれています。データ数が奇数の場合は中央の値を返し、偶数の場合は中央の2値の小さい方を返します。
>>> median_low([1, 3, 5]) 3 >>> median_low([1, 3, 5, 7]) 3
データが離散的で、中央値が補間値よりもデータ点にある値の方が良い場合に用いてください。
- statistics.median_high(data)¶
データの大きい方の中央値(high median)を返します。もし data が空の場合、
StatisticsErrorが送出されます。 data はシーケンス型やイテラブルにもなれます。high median は必ずデータに含まれています。データ数が奇数の場合は中央の値を返し、偶数の場合は中央の2値の大きい方を返します。
>>> median_high([1, 3, 5]) 3 >>> median_high([1, 3, 5, 7]) 5
データが離散的で、中央値が補間値よりもデータ点にある値の方が良い場合に用いてください。
- statistics.median_grouped(data, interval=1.0)¶
Estimates the median for numeric data that has been grouped or binned around the midpoints of consecutive, fixed-width intervals.
The data can be any iterable of numeric data with each value being exactly the midpoint of a bin. At least one value must be present.
The interval is the width of each bin.
For example, demographic information may have been summarized into consecutive ten-year age groups with each group being represented by the 5-year midpoints of the intervals:
>>> from collections import Counter >>> demographics = Counter({ ... 25: 172, # 20 to 30 years old ... 35: 484, # 30 to 40 years old ... 45: 387, # 40 to 50 years old ... 55: 22, # 50 to 60 years old ... 65: 6, # 60 to 70 years old ... }) ...
The 50th percentile (median) is the 536th person out of the 1071 member cohort. That person is in the 30 to 40 year old age group.
The regular
median()function would assume that everyone in the tricenarian age group was exactly 35 years old. A more tenable assumption is that the 484 members of that age group are evenly distributed between 30 and 40. For that, we usemedian_grouped():>>> data = list(demographics.elements()) >>> median(data) 35 >>> round(median_grouped(data, interval=10), 1) 37.5
The caller is responsible for making sure the data points are separated by exact multiples of interval. This is essential for getting a correct result. The function does not check this precondition.
Inputs may be any numeric type that can be coerced to a float during the interpolation step.
- statistics.mode(data)¶
Return the single most common data point from discrete or nominal data. The mode (when it exists) is the most typical value and serves as a measure of central location.
If there are multiple modes with the same frequency, returns the first one encountered in the data. If the smallest or largest of those is desired instead, use
min(multimode(data))ormax(multimode(data)). If the input data is empty,StatisticsErroris raised.modeは離散データであることを想定していて、1つの値を返します。これは学校で教わるような最頻値の標準的な取扱いです:>>> mode([1, 1, 2, 3, 3, 3, 3, 4]) 3
The mode is unique in that it is the only statistic in this package that also applies to nominal (non-numeric) data:
>>> mode(["red", "blue", "blue", "red", "green", "red", "red"]) 'red'
Only hashable inputs are supported. To handle type
set, consider casting tofrozenset. To handle typelist, consider casting totuple. For mixed or nested inputs, consider using this slower quadratic algorithm that only depends on equality tests:max(data, key=data.count).バージョン 3.8 で変更: Now handles multimodal datasets by returning the first mode encountered. Formerly, it raised
StatisticsErrorwhen more than one mode was found.
- statistics.multimode(data)¶
Return a list of the most frequently occurring values in the order they were first encountered in the data. Will return more than one result if there are multiple modes or an empty list if the data is empty:
>>> multimode('aabbbbccddddeeffffgg') ['b', 'd', 'f'] >>> multimode('') []
Added in version 3.8.
- statistics.pstdev(data, mu=None)¶
母標準偏差 (母分散の平方根) を返します。引数や詳細は
pvariance()を参照してください。>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75]) 0.986893273527251
- statistics.pvariance(data, mu=None)¶
data の母分散を返します。data は実数の空でないシーケンスまたはイテラブルです。分散、すなわち2次の中心化モーメントはデータの散らばり具合の測度です。分散が大きいデータはばらつきが大きく、分散が小さいデータは平均値のまわりに固まっています。
If the optional second argument mu is given, it should be the population mean of the data. It can also be used to compute the second moment around a point that is not the mean. If it is missing or
None(the default), the arithmetic mean is automatically calculated.母集団全体から分散を計算する場合に用いてください。標本から分散を推定する場合は
variance()を使いましょう。data が空の場合
StatisticsErrorを送出します。例:
>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25] >>> pvariance(data) 1.25
既にデータの平均値を計算している場合、それを第2引数 mu に渡して再計算を避けることが出来ます:
>>> mu = mean(data) >>> pvariance(data, mu) 1.25
Decimal と Fraction がサポートされています:
>>> from decimal import Decimal as D >>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")]) Decimal('24.815') >>> from fractions import Fraction as F >>> pvariance([F(1, 4), F(5, 4), F(1, 2)]) Fraction(13, 72)
注釈
母集団全体で呼んだ場合は母分散 σ² を返します。代わりに標本で呼んだ場合は biased variance s²、すなわち自由度 N の分散を返します。
If you somehow know the true population mean μ, you may use this function to calculate the variance of a sample, giving the known population mean as the second argument. Provided the data points are a random sample of the population, the result will be an unbiased estimate of the population variance.
- statistics.stdev(data, xbar=None)¶
標本標準偏差 (標本分散の平方根) を返します。引数や詳細は
variance()を参照してください。>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75]) 1.0810874155219827
- statistics.variance(data, xbar=None)¶
data の標本分散を返します。data は少なくとも2つの実数の iterable です。分散、すなわち2次の中心化モーメントはデータの散らばり具合の測度です。分散が大きいデータはばらつきが大きく、分散が小さいデータは平均値のまわりに固まっています。
If the optional second argument xbar is given, it should be the sample mean of data. If it is missing or
None(the default), the mean is automatically calculated.データが母集団の標本であるときに用いてください。母集団全体から分散を計算するには
pvariance()を参照してください。data の値が2より少ない場合
StatisticsErrorを送出します。例:
>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5] >>> variance(data) 1.3720238095238095
If you have already calculated the sample mean of your data, you can pass it as the optional second argument xbar to avoid recalculation:
>>> m = mean(data) >>> variance(data, m) 1.3720238095238095
この関数は引数として渡した xbar が実際の平均値かどうかチェックしません。任意の値を xbar に渡すと無効な結果やありえない結果が返ることがあります。
Decimal と Fraction がサポートされています:
>>> from decimal import Decimal as D >>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")]) Decimal('31.01875') >>> from fractions import Fraction as F >>> variance([F(1, 6), F(1, 2), F(5, 3)]) Fraction(67, 108)
注釈
Bessel 補正済みの標本分散 s²、すなわち自由度 N-1 の分散です。与えられたデータ点が代表的 (たとえば独立で均等に分布) な場合、戻り値は母分散の不偏推定量になります。
何らかの方法で真の母平均 μ を知っている場合、それを
pvariance()の引数 mu に渡して標本の分散を計算することが出来ます。
- statistics.quantiles(data, *, n=4, method='exclusive')¶
Divide data into n continuous intervals with equal probability. Returns a list of
n - 1cut points separating the intervals.Set n to 4 for quartiles (the default). Set n to 10 for deciles. Set n to 100 for percentiles which gives the 99 cuts points that separate data into 100 equal sized groups. Raises
StatisticsErrorif n is not least 1.The data can be any iterable containing sample data. For meaningful results, the number of data points in data should be larger than n. Raises
StatisticsErrorif there are not at least two data points.The cut points are linearly interpolated from the two nearest data points. For example, if a cut point falls one-third of the distance between two sample values,
100and112, the cut-point will evaluate to104.The method for computing quantiles can be varied depending on whether the data includes or excludes the lowest and highest possible values from the population.
The default method is "exclusive" and is used for data sampled from a population that can have more extreme values than found in the samples. The portion of the population falling below the i-th of m sorted data points is computed as
i / (m + 1). Given nine sample values, the method sorts them and assigns the following percentiles: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%.Setting the method to "inclusive" is used for describing population data or for samples that are known to include the most extreme values from the population. The minimum value in data is treated as the 0th percentile and the maximum value is treated as the 100th percentile. The portion of the population falling below the i-th of m sorted data points is computed as
(i - 1) / (m - 1). Given 11 sample values, the method sorts them and assigns the following percentiles: 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100%.# Decile cut points for empirically sampled data >>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110, ... 100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129, ... 106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86, ... 111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95, ... 103, 107, 101, 81, 109, 104] >>> [round(q, 1) for q in quantiles(data, n=10)] [81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]
Added in version 3.8.
- statistics.covariance(x, y, /)¶
Return the sample covariance of two inputs x and y. Covariance is a measure of the joint variability of two inputs.
Both inputs must be of the same length (no less than two), otherwise
StatisticsErroris raised.例:
>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9] >>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3] >>> covariance(x, y) 0.75 >>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1] >>> covariance(x, z) -7.5 >>> covariance(z, x) -7.5
Added in version 3.10.
- statistics.correlation(x, y, /, *, method='linear')¶
Return the Pearson's correlation coefficient for two inputs. Pearson's correlation coefficient r takes values between -1 and +1. It measures the strength and direction of a linear relationship.
If method is "ranked", computes Spearman's rank correlation coefficient for two inputs. The data is replaced by ranks. Ties are averaged so that equal values receive the same rank. The resulting coefficient measures the strength of a monotonic relationship.
Spearman's correlation coefficient is appropriate for ordinal data or for continuous data that doesn't meet the linear proportion requirement for Pearson's correlation coefficient.
Both inputs must be of the same length (no less than two), and need not to be constant, otherwise
StatisticsErroris raised.Example with Kepler's laws of planetary motion:
>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune >>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190] # days >>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km >>> # Show that a perfect monotonic relationship exists >>> correlation(orbital_period, dist_from_sun, method='ranked') 1.0 >>> # Observe that a linear relationship is imperfect >>> round(correlation(orbital_period, dist_from_sun), 4) 0.9882 >>> # Demonstrate Kepler's third law: There is a linear correlation >>> # between the square of the orbital period and the cube of the >>> # distance from the sun. >>> period_squared = [p * p for p in orbital_period] >>> dist_cubed = [d * d * d for d in dist_from_sun] >>> round(correlation(period_squared, dist_cubed), 4) 1.0
Added in version 3.10.
バージョン 3.12 で変更: Added support for Spearman's rank correlation coefficient.
- statistics.linear_regression(x, y, /, *, proportional=False)¶
Return the slope and intercept of simple linear regression parameters estimated using ordinary least squares. Simple linear regression describes the relationship between an independent variable x and a dependent variable y in terms of this linear function:
y = slope * x + intercept + noise
where
slopeandinterceptare the regression parameters that are estimated, andnoiserepresents the variability of the data that was not explained by the linear regression (it is equal to the difference between predicted and actual values of the dependent variable).Both inputs must be of the same length (no less than two), and the independent variable x cannot be constant; otherwise a
StatisticsErroris raised.For example, we can use the release dates of the Monty Python films to predict the cumulative number of Monty Python films that would have been produced by 2019 assuming that they had kept the pace.
>>> year = [1971, 1975, 1979, 1982, 1983] >>> films_total = [1, 2, 3, 4, 5] >>> slope, intercept = linear_regression(year, films_total) >>> round(slope * 2019 + intercept) 16
If proportional is true, the independent variable x and the dependent variable y are assumed to be directly proportional. The data is fit to a line passing through the origin. Since the intercept will always be 0.0, the underlying linear function simplifies to:
y = slope * x + noise
Continuing the example from
correlation(), we look to see how well a model based on major planets can predict the orbital distances for dwarf planets:>>> model = linear_regression(period_squared, dist_cubed, proportional=True) >>> slope = model.slope >>> # Dwarf planets: Pluto, Eris, Makemake, Haumea, Ceres >>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680] # days >>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods] >>> list(map(round, predicted_dist)) [5912, 10166, 6806, 6459, 414] >>> [5_906, 10_152, 6_796, 6_450, 414] # actual distance in million km [5906, 10152, 6796, 6450, 414]
Added in version 3.10.
バージョン 3.11 で変更: Added support for proportional.
例外¶
例外が1つ定義されています:
- exception statistics.StatisticsError¶
統計関係の例外。
ValueErrorの派生クラス。
NormalDist オブジェクト¶
NormalDist is a tool for creating and manipulating normal
distributions of a random variable. It is a
class that treats the mean and standard deviation of data
measurements as a single entity.
Normal distributions arise from the Central Limit Theorem and have a wide range of applications in statistics.
- class statistics.NormalDist(mu=0.0, sigma=1.0)¶
Returns a new NormalDist object where mu represents the arithmetic mean and sigma represents the standard deviation.
sigma が負の数の場合
StatisticsErrorを送出します。- mean¶
A read-only property for the arithmetic mean of a normal distribution.
- stdev¶
A read-only property for the standard deviation of a normal distribution.
- variance¶
A read-only property for the variance of a normal distribution. Equal to the square of the standard deviation.
- classmethod from_samples(data)¶
Makes a normal distribution instance with mu and sigma parameters estimated from the data using
fmean()andstdev().The data can be any iterable and should consist of values that can be converted to type
float. If data does not contain at least two elements, raisesStatisticsErrorbecause it takes at least one point to estimate a central value and at least two points to estimate dispersion.
- samples(n, *, seed=None)¶
Generates n random samples for a given mean and standard deviation. Returns a
listoffloatvalues.If seed is given, creates a new instance of the underlying random number generator. This is useful for creating reproducible results, even in a multi-threading context.
- pdf(x)¶
Using a probability density function (pdf), compute the relative likelihood that a random variable X will be near the given value x. Mathematically, it is the limit of the ratio
P(x <= X < x+dx) / dxas dx approaches zero.The relative likelihood is computed as the probability of a sample occurring in a narrow range divided by the width of the range (hence the word "density"). Since the likelihood is relative to other points, its value can be greater than
1.0.
- cdf(x)¶
Using a cumulative distribution function (cdf), compute the probability that a random variable X will be less than or equal to x. Mathematically, it is written
P(X <= x).
- inv_cdf(p)¶
Compute the inverse cumulative distribution function, also known as the quantile function or the percent-point function. Mathematically, it is written
x : P(X <= x) = p.Finds the value x of the random variable X such that the probability of the variable being less than or equal to that value equals the given probability p.
- overlap(other)¶
Measures the agreement between two normal probability distributions. Returns a value between 0.0 and 1.0 giving the overlapping area for the two probability density functions.
- quantiles(n=4)¶
Divide the normal distribution into n continuous intervals with equal probability. Returns a list of (n - 1) cut points separating the intervals.
Set n to 4 for quartiles (the default). Set n to 10 for deciles. Set n to 100 for percentiles which gives the 99 cuts points that separate the normal distribution into 100 equal sized groups.
- zscore(x)¶
Compute the Standard Score describing x in terms of the number of standard deviations above or below the mean of the normal distribution:
(x - mean) / stdev.Added in version 3.9.
Instances of
NormalDistsupport addition, subtraction, multiplication and division by a constant. These operations are used for translation and scaling. For example:>>> temperature_february = NormalDist(5, 2.5) # Celsius >>> temperature_february * (9/5) + 32 # Fahrenheit NormalDist(mu=41.0, sigma=4.5)
Dividing a constant by an instance of
NormalDistis not supported because the result wouldn't be normally distributed.Since normal distributions arise from additive effects of independent variables, it is possible to add and subtract two independent normally distributed random variables represented as instances of
NormalDist. For example:>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5]) >>> drug_effects = NormalDist(0.4, 0.15) >>> combined = birth_weights + drug_effects >>> round(combined.mean, 1) 3.1 >>> round(combined.stdev, 1) 0.5
Added in version 3.8.
例とレシピ¶
Classic probability problems¶
NormalDist readily solves classic probability problems.
For example, given historical data for SAT exams showing that scores are normally distributed with a mean of 1060 and a standard deviation of 195, determine the percentage of students with test scores between 1100 and 1200, after rounding to the nearest whole number:
>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4
Find the quartiles and deciles for the SAT scores:
>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]
Monte Carlo inputs for simulations¶
To estimate the distribution for a model that isn't easy to solve
analytically, NormalDist can generate input samples for a Monte
Carlo simulation:
>>> def model(x, y, z):
... return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]
Approximating binomial distributions¶
Normal distributions can be used to approximate Binomial distributions when the sample size is large and when the probability of a successful trial is near 50%.
For example, an open source conference has 750 attendees and two rooms with a 500 person capacity. There is a talk about Python and another about Ruby. In previous conferences, 65% of the attendees preferred to listen to Python talks. Assuming the population preferences haven't changed, what is the probability that the Python room will stay within its capacity limits?
>>> n = 750 # Sample size
>>> p = 0.65 # Preference for Python
>>> q = 1.0 - p # Preference for Ruby
>>> k = 500 # Room capacity
>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402
>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402
>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406
Naive bayesian classifier¶
Normal distributions commonly arise in machine learning problems.
Wikipedia has a nice example of a Naive Bayesian Classifier. The challenge is to predict a person's gender from measurements of normally distributed features including height, weight, and foot size.
We're given a training dataset with measurements for eight people. The
measurements are assumed to be normally distributed, so we summarize the data
with NormalDist:
>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])
Next, we encounter a new person whose feature measurements are known but whose gender is unknown:
>>> ht = 6.0 # height
>>> wt = 130 # weight
>>> fs = 8 # foot size
Starting with a 50% prior probability of being male or female, we compute the posterior as the prior times the product of likelihoods for the feature measurements given the gender:
>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
... weight_male.pdf(wt) * foot_size_male.pdf(fs))
>>> posterior_female = (prior_female * height_female.pdf(ht) *
... weight_female.pdf(wt) * foot_size_female.pdf(fs))
The final prediction goes to the largest posterior. This is known as the maximum a posteriori or MAP:
>>> 'male' if posterior_male > posterior_female else 'female'
'female'
Kernel density estimation¶
It is possible to estimate a continuous probability distribution from a fixed number of discrete samples.
The basic idea is to smooth the data using a kernel function such as a
normal distribution, triangular distribution, or uniform distribution.
The degree of smoothing is controlled by a scaling parameter, h,
which is called the bandwidth.
from random import choice, random
def kde_normal(data, h):
"Create a continuous probability distribution from discrete samples."
# Smooth the data with a normal distribution kernel scaled by h.
K_h = NormalDist(0.0, h)
def pdf(x):
'Probability density function. P(x <= X < x+dx) / dx'
return sum(K_h.pdf(x - x_i) for x_i in data) / len(data)
def cdf(x):
'Cumulative distribution function. P(X <= x)'
return sum(K_h.cdf(x - x_i) for x_i in data) / len(data)
def rand():
'Random selection from the probability distribution.'
return choice(data) + K_h.inv_cdf(random())
return pdf, cdf, rand
Wikipedia has an example
where we can use the kde_normal() recipe to generate and plot
a probability density function estimated from a small sample:
>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> pdf, cdf, rand = kde_normal(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [pdf(x) for x in xarr]
The points in xarr and yarr can be used to make a PDF plot:
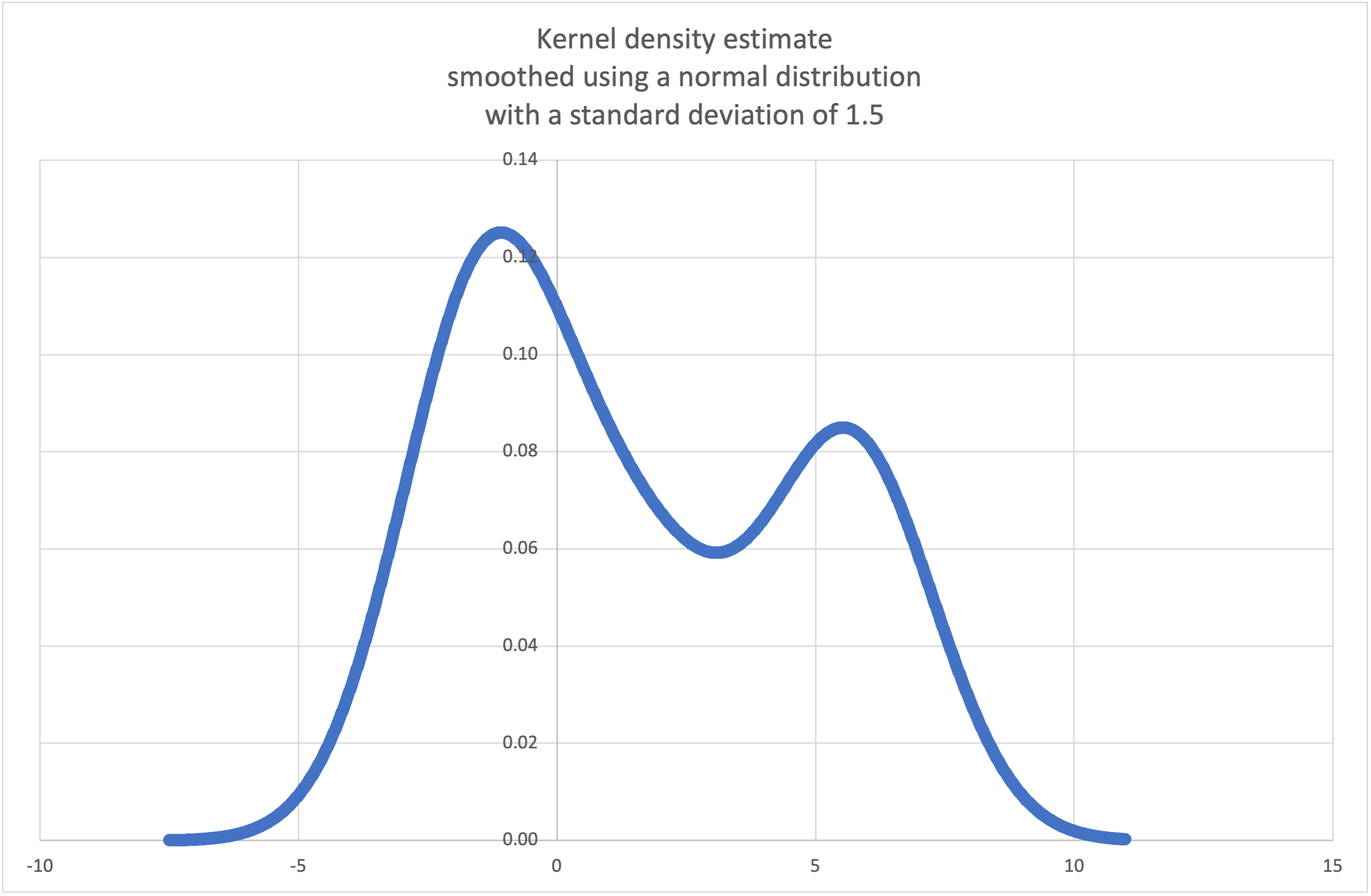
Resample the data to produce 100 new selections:
>>> new_selections = [rand() for i in range(100)]
Determine the probability of a new selection being below 2.0:
>>> round(cdf(2.0), 4)
0.5794
Add a new sample data point and find the new CDF at 2.0:
>>> sample.append(4.9)
>>> round(cdf(2.0), 4)
0.5005