statistics --- Mathematical statistics functions¶
Ajouté dans la version 3.4.
Code source : Lib/statistics.py
Ce module fournit des fonctions pour le calcul de valeurs statistiques sur des données numériques (valeurs réelles de la classe Real).
The module is not intended to be a competitor to third-party libraries such as NumPy, SciPy, or proprietary full-featured statistics packages aimed at professional statisticians such as Minitab, SAS and Matlab. It is aimed at the level of graphing and scientific calculators.
À moins que cela ne soit précisé différemment, ces fonctions gèrent les objets int, float, Decimal et Fraction. Leur bon comportement avec d'autres types (numériques ou non) n'est pas garanti. Le comportement de ces fonctions sur des collections mixtes de différents types est indéfini et dépend de l'implémentation. Si vos données comportement un mélange de plusieurs types, vous pouvez utiliser map() pour vous assurer que le résultat est cohérent, par exemple : map(float, input_data).
Some datasets use NaN (not a number) values to represent missing data.
Since NaNs have unusual comparison semantics, they cause surprising or
undefined behaviors in the statistics functions that sort data or that count
occurrences. The functions affected are median(), median_low(),
median_high(), median_grouped(), mode(), multimode(), and
quantiles(). The NaN values should be stripped before calling these
functions:
>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse
>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data) # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data) # This result is unexpected
16.35
>>> sum(map(isnan, data)) # Number of missing values
2
>>> clean = list(filterfalse(isnan, data)) # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean) # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean) # This result is now well defined
18.75
Moyennes et mesures de la tendance centrale¶
Ces fonctions calculent une moyenne ou une valeur typique à partir d'une population ou d'un échantillon.
Moyenne arithmétique des données. |
|
Fast, floating-point arithmetic mean, with optional weighting. |
|
Moyenne géométrique des données. |
|
Moyenne harmonique des données. |
|
Médiane (valeur centrale) des données. |
|
Médiane basse des données. |
|
Médiane haute des données. |
|
Median (50th percentile) of grouped data. |
|
Mode principal (la valeur la plus représentée) de données discrètes ou nominales. |
|
Liste des modes (les valeurs les plus représentées) de données discrètes ou nominales. |
|
Divise les données en intervalles de même probabilité. |
Mesures de la dispersion¶
Ces fonctions mesurent la tendance de la population ou d'un échantillon à dévier des valeurs typiques ou des valeurs moyennes.
Écart-type de la population. |
|
Variance de la population. |
|
Écart-type d'un échantillon. |
|
Variance d'un échantillon. |
Statistics for relations between two inputs¶
These functions calculate statistics regarding relations between two inputs.
Covariance d'un échantillon pour deux variables. |
|
Pearson and Spearman's correlation coefficients. |
|
Slope and intercept for simple linear regression. |
Détails des fonctions¶
Note : les fonctions ne requièrent pas que les données soient ordonnées. Toutefois, pour en faciliter la lecture, les exemples utiliseront des séquences croissantes.
- statistics.mean(data)¶
Renvoie la moyenne arithmétique de l'échantillon data qui peut être une séquence ou un itérable.
La moyenne arithmétique est la somme des valeurs divisée par le nombre d'observations. Il s'agit de la valeur couramment désignée comme la « moyenne » bien qu'il existe de multiples façons de définir mathématiquement la moyenne. C'est une mesure de la tendance centrale des données.
Une erreur
StatisticsErrorest levée si data est vide.Exemples d'utilisation :
>>> mean([1, 2, 3, 4, 4]) 2.8 >>> mean([-1.0, 2.5, 3.25, 5.75]) 2.625 >>> from fractions import Fraction as F >>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)]) Fraction(13, 21) >>> from decimal import Decimal as D >>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")]) Decimal('0.5625')
Note
La moyenne arithmétique est fortement impactée par la présence de valeurs aberrantes et n'est pas un estimateur robuste de la tendance centrale : la moyenne n'est pas nécessairement un exemple représentatif de l'échantillon. Voir
median()pour des mesures plus robustes de la tendance centrale.La moyenne de l'échantillon est une estimation non biaisée de la moyenne de la véritable population. Ainsi, en calculant la moyenne sur tous les échantillons possibles,
mean(sample)converge vers la moyenne réelle de la population entière. Si data est une population entière plutôt qu'un échantillon, alorsmean(data)équivaut à calculer la véritable moyenne μ.
- statistics.fmean(data, weights=None)¶
Convertit data en nombres à virgule flottante et calcule la moyenne arithmétique.
Cette fonction est plus rapide que
mean()et renvoie toujours unfloat. data peut être une séquence ou un itérable. Si les données d'entrée sont vides, la fonction lève une erreurStatisticsError.>>> fmean([3.5, 4.0, 5.25]) 4.25
Optional weighting is supported. For example, a professor assigns a grade for a course by weighting quizzes at 20%, homework at 20%, a midterm exam at 30%, and a final exam at 30%:
>>> grades = [85, 92, 83, 91] >>> weights = [0.20, 0.20, 0.30, 0.30] >>> fmean(grades, weights) 87.6
If weights is supplied, it must be the same length as the data or a
ValueErrorwill be raised.Ajouté dans la version 3.8.
Modifié dans la version 3.11: Added support for weights.
- statistics.geometric_mean(data)¶
Convertit data en nombres à virgule flottante et calcule la moyenne géométrique.
La moyenne géométrique mesure la tendance centrale ou la valeur typique de data en utilisant le produit des valeurs (par opposition à la moyenne arithmétique qui utilise la somme).
Lève une erreur
StatisticsErrorsi les données sont vides, si elles contiennent un zéro ou une valeur négative. data peut être une séquence ou un itérable.Aucune mesure particulière n'est prise pour garantir que le résultat est parfaitement exact (cela peut toutefois changer dans une version future).
>>> round(geometric_mean([54, 24, 36]), 1) 36.0
Ajouté dans la version 3.8.
- statistics.harmonic_mean(data, weights=None)¶
Return the harmonic mean of data, a sequence or iterable of real-valued numbers. If weights is omitted or
None, then equal weighting is assumed.The harmonic mean is the reciprocal of the arithmetic
mean()of the reciprocals of the data. For example, the harmonic mean of three values a, b and c will be equivalent to3/(1/a + 1/b + 1/c). If one of the values is zero, the result will be zero.The harmonic mean is a type of average, a measure of the central location of the data. It is often appropriate when averaging ratios or rates, for example speeds.
Supposons qu'une voiture parcoure 10 km à 40 km/h puis 10 km à 60 km/h. Quelle a été sa vitesse moyenne ?
>>> harmonic_mean([40, 60]) 48.0
Suppose a car travels 40 km/hr for 5 km, and when traffic clears, speeds-up to 60 km/hr for the remaining 30 km of the journey. What is the average speed?
>>> harmonic_mean([40, 60], weights=[5, 30]) 56.0
StatisticsErroris raised if data is empty, any element is less than zero, or if the weighted sum isn't positive.L'algorithme actuellement implémenté s'arrête prématurément lors de la rencontre d'un zéro dans le parcours de l'entrée. Cela signifie que la validité des valeurs suivantes n'est pas testée (ce comportement est susceptible de changer dans une version future).
Ajouté dans la version 3.6.
Modifié dans la version 3.10: Added support for weights.
- statistics.median(data)¶
Renvoie la médiane (la valeur centrale) de données numériques en utilisant la méthode classique « moyenne des deux du milieu ». Lève une erreur
StatisticsErrorsi data est vide. data peut être une séquence ou un itérable.La médiane est une mesure robuste de la tendance centrale et est moins sensible à la présence de valeurs aberrantes que la moyenne. Lorsque le nombre d'observations est impair, la valeur du milieu est renvoyée :
>>> median([1, 3, 5]) 3
Lorsque le nombre d'observations est pair, la médiane est interpolée en calculant la moyenne des deux valeurs du milieu :
>>> median([1, 3, 5, 7]) 4.0
Cette approche est adaptée à des données discrètes à condition que vous acceptiez que la médiane ne fasse pas nécessairement partie des observations.
Si les données sont ordinales (elles peuvent être ordonnées) mais pas numériques (elles ne peuvent être additionnées), utilisez
median_low()oumedian_high()à la place.
- statistics.median_low(data)¶
Renvoie la médiane basse de données numériques. Lève une erreur
StatisticsErrorsi data est vide. data peut être une séquence ou un itérable.La médiane basse est toujours une valeur représentée dans les données. Lorsque le nombre d'observations est impair, la valeur du milieu est renvoyée. Sinon, la plus petite des deux valeurs du milieu est renvoyée.
>>> median_low([1, 3, 5]) 3 >>> median_low([1, 3, 5, 7]) 3
Utilisez la médiane basse lorsque vos données sont discrètes et que vous préférez que la médiane soit une valeur représentée dans vos observations plutôt que le résultat d'une interpolation.
- statistics.median_high(data)¶
Renvoie la médiane haute des données. Lève une erreur
StatisticsErrorsi data est vide. data peut être une séquence ou un itérable.La médiane haute est toujours une valeur représentée dans les données. Lorsque le nombre d'observations est impair, la valeur du milieu est renvoyée. Sinon, la plus grande des deux valeurs du milieu est renvoyée.
>>> median_high([1, 3, 5]) 3 >>> median_high([1, 3, 5, 7]) 5
Utilisez la médiane haute lorsque vos données sont discrètes et que vous préférez que la médiane soit une valeur représentée dans vos observations plutôt que le résultat d'une interpolation.
- statistics.median_grouped(data, interval=1.0)¶
Estimates the median for numeric data that has been grouped or binned around the midpoints of consecutive, fixed-width intervals.
The data can be any iterable of numeric data with each value being exactly the midpoint of a bin. At least one value must be present.
The interval is the width of each bin.
For example, demographic information may have been summarized into consecutive ten-year age groups with each group being represented by the 5-year midpoints of the intervals:
>>> from collections import Counter >>> demographics = Counter({ ... 25: 172, # 20 to 30 years old ... 35: 484, # 30 to 40 years old ... 45: 387, # 40 to 50 years old ... 55: 22, # 50 to 60 years old ... 65: 6, # 60 to 70 years old ... }) ...
The 50th percentile (median) is the 536th person out of the 1071 member cohort. That person is in the 30 to 40 year old age group.
The regular
median()function would assume that everyone in the tricenarian age group was exactly 35 years old. A more tenable assumption is that the 484 members of that age group are evenly distributed between 30 and 40. For that, we usemedian_grouped():>>> data = list(demographics.elements()) >>> median(data) 35 >>> round(median_grouped(data, interval=10), 1) 37.5
The caller is responsible for making sure the data points are separated by exact multiples of interval. This is essential for getting a correct result. The function does not check this precondition.
Inputs may be any numeric type that can be coerced to a float during the interpolation step.
- statistics.mode(data)¶
Renvoie la valeur la plus représentée dans la collection data (discrète ou nominale). Ce mode, lorsqu'il existe, est la valeur la plus représentative des données et est une mesure de la tendance centrale.
S'il existe plusieurs modes avec la même fréquence, cette fonction renvoie le premier qui a été rencontré dans data. Utilisez
min(multimode(data))oumax(multimode(data))si vous désirez le plus petit mode ou le plus grand mode. Lève une erreurStatisticsErrorsi data est vide.modesuppose que les données sont discrètes et renvoie une seule valeur. Il s'agit de la définition usuelle du mode telle qu'enseignée dans à l'école :>>> mode([1, 1, 2, 3, 3, 3, 3, 4]) 3
Le mode a la particularité d'être la seule statistique de ce module à pouvoir être calculée sur des données nominales (non numériques) :
>>> mode(["red", "blue", "blue", "red", "green", "red", "red"]) 'red'
Only hashable inputs are supported. To handle type
set, consider casting tofrozenset. To handle typelist, consider casting totuple. For mixed or nested inputs, consider using this slower quadratic algorithm that only depends on equality tests:max(data, key=data.count).Modifié dans la version 3.8: Gère désormais des jeux de données avec plusieurs modes en renvoyant le premier mode rencontré. Précédemment, une erreur
StatisticsErrorétait levée si plusieurs modes étaient trouvés.
- statistics.multimode(data)¶
Renvoie une liste des valeurs les plus fréquentes en suivant leur ordre d'apparition dans data. Renvoie plusieurs résultats s'il y a plusieurs modes ou une liste vide si data est vide :
>>> multimode('aabbbbccddddeeffffgg') ['b', 'd', 'f'] >>> multimode('') []
Ajouté dans la version 3.8.
- statistics.pstdev(data, mu=None)¶
Renvoie l'écart-type de la population (racine carrée de la variance de la population). Voir
pvariance()pour les arguments et d'autres précisions.>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75]) 0.986893273527251
- statistics.pvariance(data, mu=None)¶
Renvoie la variance de la population data, une séquence non-vide ou un itérable de valeurs réelles. La variance, ou moment de second ordre, est une mesure de la variabilité (ou dispersion) des données. Une variance élevée indique une large dispersion des valeurs ; une faible variance indique que les valeurs sont resserrées autour de la moyenne.
If the optional second argument mu is given, it should be the population mean of the data. It can also be used to compute the second moment around a point that is not the mean. If it is missing or
None(the default), the arithmetic mean is automatically calculated.Utilisez cette fonction pour calculer la variance sur une population complète. Pour estimer la variance à partir d'un échantillon, utilisez plutôt
variance()à la place.Lève une erreur
StatisticsErrorsi data est vide.Exemples :
>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25] >>> pvariance(data) 1.25
Si vous connaissez la moyenne de vos données, il est possible de la passer comme argument optionnel mu lors de l'appel de fonction pour éviter de la calculer une nouvelle fois :
>>> mu = mean(data) >>> pvariance(data, mu) 1.25
La fonction gère les nombres décimaux et les fractions :
>>> from decimal import Decimal as D >>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")]) Decimal('24.815') >>> from fractions import Fraction as F >>> pvariance([F(1, 4), F(5, 4), F(1, 2)]) Fraction(13, 72)
Note
Cette fonction renvoie la variance de la population σ² lorsqu'elle est appliquée sur la population entière. Si elle est appliquée seulement sur un échantillon, le résultat est alors la variance de l'échantillon s² ou variance à N degrés de liberté.
Si vous connaissez d'avance la vraie moyenne de la population μ, vous pouvez utiliser cette fonction pour calculer la variance de l'échantillon sachant la moyenne de la population en la passante comme second argument. En supposant que les observations sont issues d'un tirage aléatoire uniforme dans la population, le résultat sera une estimation non biaisée de la variance de la population.
- statistics.stdev(data, xbar=None)¶
Renvoie l'écart-type de l'échantillon (racine carrée de la variance de l'échantillon). Voir
variance()pour les arguments et plus de détails.>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75]) 1.0810874155219827
- statistics.variance(data, xbar=None)¶
Renvoie la variance de l'échantillon data, un itérable d'au moins deux valeurs réelles. La variance, ou moment de second ordre, est une mesure de la variabilité (ou dispersion) des données. Une variance élevée indique que les données sont très dispersées ; une variance faible indique que les valeurs sont resserrées autour de la moyenne.
If the optional second argument xbar is given, it should be the sample mean of data. If it is missing or
None(the default), the mean is automatically calculated.Utilisez cette fonction lorsque vos données forment un échantillon d'une population plus grande. Pour calculer la variance d'une population complète, utilisez
pvariance().Lève une erreur
StatisticsErrorsi data contient moins de deux éléments.Exemples :
>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5] >>> variance(data) 1.3720238095238095
If you have already calculated the sample mean of your data, you can pass it as the optional second argument xbar to avoid recalculation:
>>> m = mean(data) >>> variance(data, m) 1.3720238095238095
Cette fonction ne vérifie pas que la valeur passée dans l'argument xbar correspond bien à la moyenne. Utiliser des valeurs arbitraires pour xbar produit des résultats impossibles ou incorrects.
La fonction gère les nombres décimaux et les fractions :
>>> from decimal import Decimal as D >>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")]) Decimal('31.01875') >>> from fractions import Fraction as F >>> variance([F(1, 6), F(1, 2), F(5, 3)]) Fraction(67, 108)
Note
Cela correspond à la variance s² de l'échantillon avec correction de Bessel (ou variance à N-1 degrés de liberté). En supposant que les observations sont représentatives de la population (c'est-à-dire indépendantes et identiquement distribuées), alors le résultat est une estimation non biaisée de la variance.
Si vous connaissez d'avance la vraie moyenne μ de la population, vous devriez la passer à
pvariance()comme paramètre mu pour obtenir la variance de l'échantillon.
- statistics.quantiles(data, *, n=4, method='exclusive')¶
Divise data en n intervalles réels de même probabilité. Renvoie une liste de
n - 1valeurs délimitant les intervalles (les quantiles).Utilisez
n = 4pour obtenir les quartiles (le défaut),n = 10pour obtenir les déciles etn = 100pour obtenir les centiles (ce qui produit 99 valeurs qui séparent data en 100 groupes de même taille). Lève une erreurStatisticsErrorsi n est strictement inférieur à 1.data peut être n'importe quel itérable contenant les valeurs de l'échantillon. Pour que les résultats aient un sens, le nombre d'observations dans l'échantillon data doit être plus grand que n. Lève une erreur
StatisticsErrors'il n'y a pas au moins deux observations.Les quantiles sont linéairement interpolées à partir des deux valeurs les plus proches dans l'échantillon. Par exemple, si un quantile se situe à un tiers de la distance entre les deux valeurs de l'échantillon
100et112, le quantile vaudra104.L'argument method indique la méthode à utiliser pour calculer les quantiles et peut être modifié pour spécifier s'il faut inclure ou exclure les valeurs basses et hautes de data de la population.
La valeur par défaut pour method est
"exclusive"et est applicable pour des données échantillonnées dans une population dont une des valeurs extrêmes peut être plus grande (respectivement plus petite) que le maximum (respectivement le minimum) des valeurs de l'échantillon. La proportion de la population se situant en-dessous du ie de m valeurs ordonnées est calculée par la formulei / (m + 1). Par exemple, en supposant 9 valeurs dans l'échantillon, cette méthode les ordonne et leur associe les quantiles suivants : 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%.En utilisant
"inclusive"comme valeur du paramètre method, on suppose que data correspond soit à une population entière, soit que les valeurs extrêmes de la population sont représentées dans l'échantillon. Le minimum de data est alors considéré comme 0e centile et le maximum comme 100e centile. La proportion de la population se situant sous la ie valeur de m valeurs ordonnées est calculée par la formule(i - 1)/(m - 1). En supposant que l'on a 11 valeurs dans l'échantillon, cette méthode les ordonne et leur associe les quantiles suivants : 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100%.# Decile cut points for empirically sampled data >>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110, ... 100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129, ... 106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86, ... 111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95, ... 103, 107, 101, 81, 109, 104] >>> [round(q, 1) for q in quantiles(data, n=10)] [81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]
Ajouté dans la version 3.8.
- statistics.covariance(x, y, /)¶
Return the sample covariance of two inputs x and y. Covariance is a measure of the joint variability of two inputs.
Both inputs must be of the same length (no less than two), otherwise
StatisticsErroris raised.Exemples :
>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9] >>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3] >>> covariance(x, y) 0.75 >>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1] >>> covariance(x, z) -7.5 >>> covariance(z, x) -7.5
Ajouté dans la version 3.10.
- statistics.correlation(x, y, /, *, method='linear')¶
Return the Pearson's correlation coefficient for two inputs. Pearson's correlation coefficient r takes values between -1 and +1. It measures the strength and direction of a linear relationship.
If method is "ranked", computes Spearman's rank correlation coefficient for two inputs. The data is replaced by ranks. Ties are averaged so that equal values receive the same rank. The resulting coefficient measures the strength of a monotonic relationship.
Spearman's correlation coefficient is appropriate for ordinal data or for continuous data that doesn't meet the linear proportion requirement for Pearson's correlation coefficient.
Both inputs must be of the same length (no less than two), and need not to be constant, otherwise
StatisticsErroris raised.Example with Kepler's laws of planetary motion:
>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune >>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190] # days >>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km >>> # Show that a perfect monotonic relationship exists >>> correlation(orbital_period, dist_from_sun, method='ranked') 1.0 >>> # Observe that a linear relationship is imperfect >>> round(correlation(orbital_period, dist_from_sun), 4) 0.9882 >>> # Demonstrate Kepler's third law: There is a linear correlation >>> # between the square of the orbital period and the cube of the >>> # distance from the sun. >>> period_squared = [p * p for p in orbital_period] >>> dist_cubed = [d * d * d for d in dist_from_sun] >>> round(correlation(period_squared, dist_cubed), 4) 1.0
Ajouté dans la version 3.10.
Modifié dans la version 3.12: Added support for Spearman's rank correlation coefficient.
- statistics.linear_regression(x, y, /, *, proportional=False)¶
Return the slope and intercept of simple linear regression parameters estimated using ordinary least squares. Simple linear regression describes the relationship between an independent variable x and a dependent variable y in terms of this linear function:
y = slope * x + intercept + noise
where
slopeandinterceptare the regression parameters that are estimated, andnoiserepresents the variability of the data that was not explained by the linear regression (it is equal to the difference between predicted and actual values of the dependent variable).Both inputs must be of the same length (no less than two), and the independent variable x cannot be constant; otherwise a
StatisticsErroris raised.For example, we can use the release dates of the Monty Python films to predict the cumulative number of Monty Python films that would have been produced by 2019 assuming that they had kept the pace.
>>> year = [1971, 1975, 1979, 1982, 1983] >>> films_total = [1, 2, 3, 4, 5] >>> slope, intercept = linear_regression(year, films_total) >>> round(slope * 2019 + intercept) 16
If proportional is true, the independent variable x and the dependent variable y are assumed to be directly proportional. The data is fit to a line passing through the origin. Since the intercept will always be 0.0, the underlying linear function simplifies to:
y = slope * x + noise
Continuing the example from
correlation(), we look to see how well a model based on major planets can predict the orbital distances for dwarf planets:>>> model = linear_regression(period_squared, dist_cubed, proportional=True) >>> slope = model.slope >>> # Dwarf planets: Pluto, Eris, Makemake, Haumea, Ceres >>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680] # days >>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods] >>> list(map(round, predicted_dist)) [5912, 10166, 6806, 6459, 414] >>> [5_906, 10_152, 6_796, 6_450, 414] # actual distance in million km [5906, 10152, 6796, 6450, 414]
Ajouté dans la version 3.10.
Modifié dans la version 3.11: Added support for proportional.
Exceptions¶
Une seule exception est définie :
- exception statistics.StatisticsError¶
Sous-classe de
ValueErrorpour les exceptions liées aux statistiques.
Objets NormalDist¶
NormalDist est un outil permettant de créer et manipuler des lois normales de variables aléatoires. Cette classe gère la moyenne et l'écart-type d'un ensemble d'observations comme une seule entité.
Les lois normales apparaissent dans de très nombreuses applications des statistiques. Leur ubiquité découle du théorème central limite.
- class statistics.NormalDist(mu=0.0, sigma=1.0)¶
Renvoie un nouvel objet NormalDist où mu représente la moyenne arithmétique et sigma l'écart-type.
Lève une erreur
StatisticsErrorsi sigma est négatif.- mean¶
Attribut en lecture seule correspondant à la moyenne arithmétique d'une loi normale.
- stdev¶
Attribut en lecture seule correspondant à l'écart-type d'une loi normale.
- variance¶
Attribut en lecture seule correspondant à la variance d'une loi normale. La variance est égale au carré de l'écart-type.
- classmethod from_samples(data)¶
Crée une instance de loi normale de paramètres mu et sigma estimés à partir de data en utilisant
fmean()etstdev().data peut être n'importe quel iterable de valeurs pouvant être converties en
float. Lève une erreurStatisticsErrorsi data ne contient pas au moins deux éléments car il faut au moins un point pour estimer la moyenne et deux points pour estimer la variance.
- samples(n, *, seed=None)¶
Génère n valeurs aléatoires suivant une loi normale de moyenne et écart-type connus. Renvoie une
listdefloat.Si seed est spécifié, sa valeur est utilisée pour initialiser une nouvelle instance du générateur de nombres aléatoires. Cela permet de produire des résultats reproductibles même dans un contexte de parallélisme par fils d'exécution.
- pdf(x)¶
Calcule la vraisemblance qu'une variable aléatoire X soit proche de la valeur x à partir de la fonction de densité. Mathématiquement, cela correspond à la limite de la fraction
P(x <= X < x + dx) / dxlorsquedxtend vers zéro.The relative likelihood is computed as the probability of a sample occurring in a narrow range divided by the width of the range (hence the word "density"). Since the likelihood is relative to other points, its value can be greater than
1.0.
- cdf(x)¶
Calcule la probabilité qu'une variable aléatoire X soit inférieure ou égale à x à partir de la fonction de répartition. Mathématiquement, cela correspond à
P(X <= x).
- inv_cdf(p)¶
Compute the inverse cumulative distribution function, also known as the quantile function or the percent-point function. Mathematically, it is written
x : P(X <= x) = p.Détermine la valeur x de la variable aléatoire X telle que la probabilité que la variable soit inférieure ou égale à cette valeur x est égale à p.
- overlap(other)¶
Mesure le recouvrement entre deux lois normales. Renvoie une valeur réelle entre 0 et 1 indiquant l'aire du recouvrement de deux densités de probabilité.
- quantiles(n=4)¶
Divise la loi normale entre n intervalles réels équiprobables. Renvoie une liste de
(n - 1)quantiles séparant les intervalles.Utilisez
n = 4pour obtenir les quartiles (le défaut),n = 10pour obtenir les déciles etn = 100pour obtenir les centiles (ce qui produit 99 valeurs qui séparent data en 100 groupes de même taille).
- zscore(x)¶
Compute the Standard Score describing x in terms of the number of standard deviations above or below the mean of the normal distribution:
(x - mean) / stdev.Ajouté dans la version 3.9.
Les instances de la classe
NormalDistgèrent l'addition, la soustraction, la multiplication et la division par une constante. Ces opérations peuvent être utilisées pour la translation ou la mise à l'échelle, par exemple :>>> temperature_february = NormalDist(5, 2.5) # Celsius >>> temperature_february * (9/5) + 32 # Fahrenheit NormalDist(mu=41.0, sigma=4.5)
Diviser une constante par une instance de
NormalDistn'est pas pris en charge car le résultat ne serait pas une loi normale.Étant donné que les lois normales sont issues des propriétés additives de variables indépendantes, il est possible d'ajouter ou de soustraite deux variables normales indépendantes représentées par des instances de
NormalDist. Par exemple :>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5]) >>> drug_effects = NormalDist(0.4, 0.15) >>> combined = birth_weights + drug_effects >>> round(combined.mean, 1) 3.1 >>> round(combined.stdev, 1) 0.5
Ajouté dans la version 3.8.
Examples and Recipes¶
Classic probability problems¶
NormalDist permet de résoudre aisément des problèmes probabilistes classiques.
Par exemple, sachant que les scores aux examens SAT suivent une loi normale de moyenne 1060 et d'écart-type 195, déterminer le pourcentage d'étudiants dont les scores se situent entre 1100 et 1200, arrondi à l'entier le plus proche :
>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4
Déterminer les quartiles et les déciles des scores SAT :
>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]
Monte Carlo inputs for simulations¶
To estimate the distribution for a model that isn't easy to solve
analytically, NormalDist can generate input samples for a Monte
Carlo simulation:
>>> def model(x, y, z):
... return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]
Approximating binomial distributions¶
Normal distributions can be used to approximate Binomial distributions when the sample size is large and when the probability of a successful trial is near 50%.
Par exemple, 750 personnes assistent à une conférence sur le logiciel libre. Il y a deux salles pouvant chacune accueillir 500 personnes. Dans la première salle a lieu une présentation sur Python, dans l'autre une présentation à propos de Ruby. Lors des conférences passées, 65% des personnes ont préféré écouter les présentations sur Python. En supposant que les préférences de la population n'ont pas changé, quelle est la probabilité que la salle Python reste en-dessous de sa capacité d'accueil ?
>>> n = 750 # Sample size
>>> p = 0.65 # Preference for Python
>>> q = 1.0 - p # Preference for Ruby
>>> k = 500 # Room capacity
>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402
>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402
>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406
Naive bayesian classifier¶
Les lois normales interviennent souvent en apprentissage automatique.
Wikipedia has a nice example of a Naive Bayesian Classifier. The challenge is to predict a person's gender from measurements of normally distributed features including height, weight, and foot size.
Nous avons à notre disposition un jeu de données d'apprentissage contenant les mesures de huit personnes. On suppose que ces mesures suivent une loi normale. Nous pouvons donc synthétiser les données à l'aide de NormalDist :
>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])
Ensuite, nous rencontrons un nouvel individu dont nous connaissons les proportions mais pas le sexe :
>>> ht = 6.0 # height
>>> wt = 130 # weight
>>> fs = 8 # foot size
En partant d'une probabilité a priori de 50% d'être un homme ou une femme, nous calculons la probabilité a posteriori comme le produit de la probabilité antérieure et de la vraisemblance des différentes mesures étant donné le sexe :
>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
... weight_male.pdf(wt) * foot_size_male.pdf(fs))
>>> posterior_female = (prior_female * height_female.pdf(ht) *
... weight_female.pdf(wt) * foot_size_female.pdf(fs))
La prédiction finale est celle qui a la plus grande probabilité a posteriori. Cette approche est appelée maximum a posteriori ou MAP :
>>> 'male' if posterior_male > posterior_female else 'female'
'female'
Kernel density estimation¶
It is possible to estimate a continuous probability distribution from a fixed number of discrete samples.
The basic idea is to smooth the data using a kernel function such as a
normal distribution, triangular distribution, or uniform distribution.
The degree of smoothing is controlled by a scaling parameter, h,
which is called the bandwidth.
from random import choice, random
def kde_normal(data, h):
"Create a continuous probability distribution from discrete samples."
# Smooth the data with a normal distribution kernel scaled by h.
K_h = NormalDist(0.0, h)
def pdf(x):
'Probability density function. P(x <= X < x+dx) / dx'
return sum(K_h.pdf(x - x_i) for x_i in data) / len(data)
def cdf(x):
'Cumulative distribution function. P(X <= x)'
return sum(K_h.cdf(x - x_i) for x_i in data) / len(data)
def rand():
'Random selection from the probability distribution.'
return choice(data) + K_h.inv_cdf(random())
return pdf, cdf, rand
Wikipedia has an example
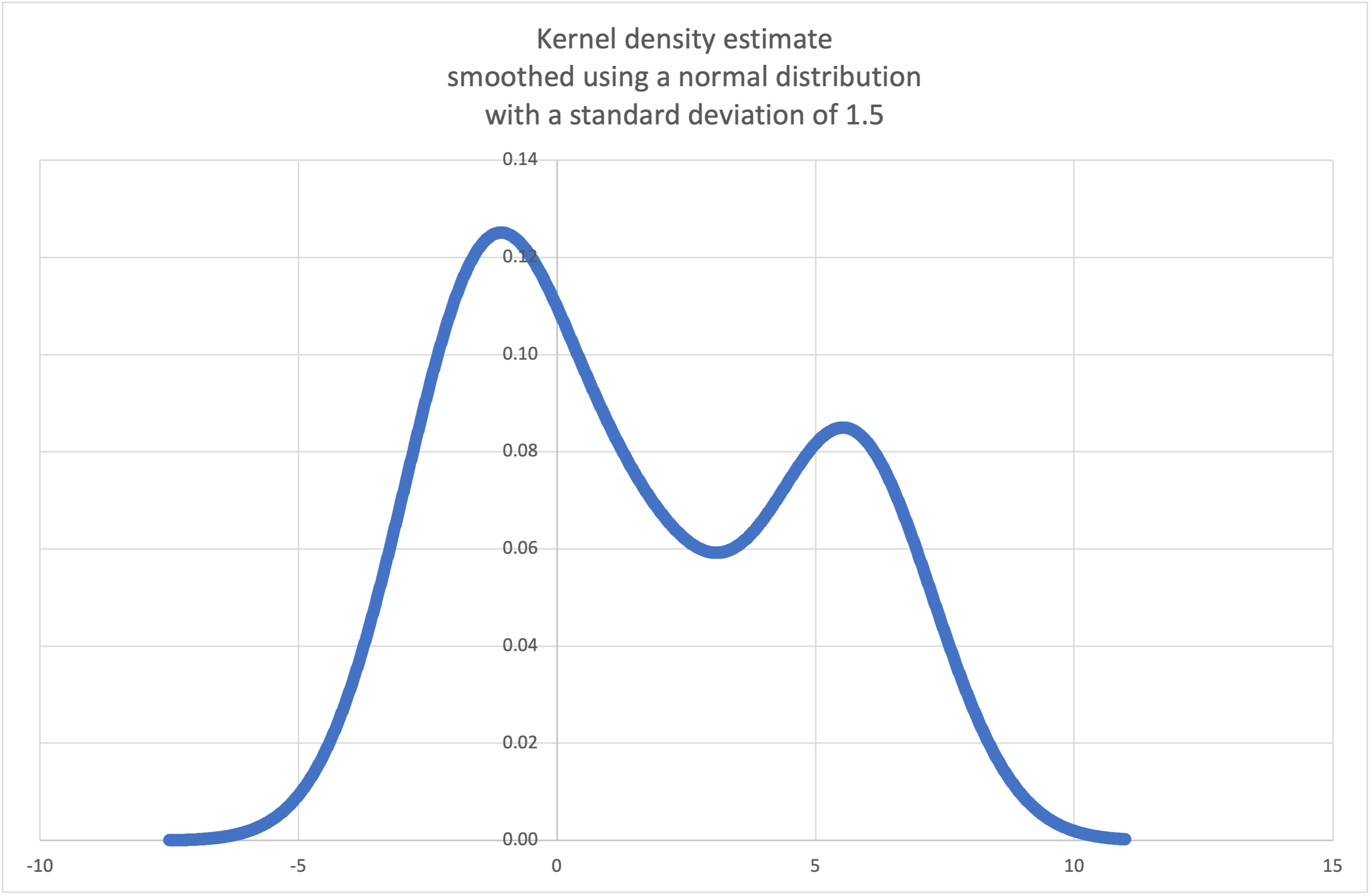
where we can use the kde_normal() recipe to generate and plot
a probability density function estimated from a small sample:
>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> pdf, cdf, rand = kde_normal(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [pdf(x) for x in xarr]
The points in xarr and yarr can be used to make a PDF plot:
Resample the data to produce 100 new selections:
>>> new_selections = [rand() for i in range(100)]
Determine the probability of a new selection being below 2.0:
>>> round(cdf(2.0), 4)
0.5794
Add a new sample data point and find the new CDF at 2.0:
>>> sample.append(4.9)
>>> round(cdf(2.0), 4)
0.5005