statistics — Mathematical statistics functions

Added in version 3.4.

Código fuente: Lib/statistics.py

---

Este módulo proporciona funciones para calcular estadísticas matemáticas de datos numéricos (de tipo Real).

Este módulo no pretende ser competidor o sustituto de bibliotecas de terceros como NumPy o SciPy, ni de paquetes completos de software propietario para estadistas profesionales como Minitab, SAS o Matlab. Este módulo se ubica a nivel de calculadoras científicas y gráficas.

A menos que se indique explícitamente lo contrario, las funciones de este módulo manejan objetos int, float, Decimal y Fraction. No se garantiza un correcto funcionamiento con otros tipos (numéricos o no). El comportamiento de estas funciones con colecciones mixtas que contengan objetos de diferente tipo no está definido y depende de la implementación. Si tus datos de entrada consisten en una mezcla de varios tipos, puedes usar map() para asegurarte de que el resultado sea consistente, por ejemplo: map(float, input_data).

Algunos conjuntos de datos utilizan valores NaN (no es un número) para representar los datos que faltan. Dado que los valores NaN tienen una semántica de comparación inusual, provocan comportamientos sorprendentes o indefinidos en las funciones estadísticas que ordenan los datos o que cuentan las ocurrencias. Las funciones afectadas son median(), median_low(), median_high(), median_grouped(), mode(), multimode(), y quantiles(). Los valores NaN deben eliminarse antes de llamar a estas funciones:

>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse

>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data)  # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data)  # This result is unexpected
16.35

>>> sum(map(isnan, data))    # Number of missing values
2
>>> clean = list(filterfalse(isnan, data))  # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean)  # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean)       # This result is now well defined
18.75

Promedios y medidas de tendencia central

Estas funciones calculan el promedio o el valor típico de una población o muestra.

mean()	Media aritmética («promedio») de los datos.
fmean()	Fast, floating-point arithmetic mean, with optional weighting.
geometric_mean()	Media geométrica de los datos.
harmonic_mean()	Media armónica de los datos.
median()	Mediana (valor central) de los datos.
median_low()	Mediana baja de los datos.
median_high()	Mediana alta de los datos.
median_grouped()	Median (50th percentile) of grouped data.
mode()	Moda única (valor más común) de datos discretos o nominales.
multimode()	Lista de modas (valores más comunes) de datos discretos o nominales.
quantiles()	Divide los datos en intervalos equiprobables.

Medidas de dispersión

Estas funciones calculan una medida de cuánto tiende a desviarse la población o muestra de los valores típicos o promedios.

pstdev()	Desviación típica poblacional de los datos.
pvariance()	Varianza poblacional de los datos.
stdev()	Desviación típica muestral de los datos.
variance()	Varianza muestral de los datos.

Estadísticas para relaciones entre dos entradas

Estas funciones calculan estadísticas sobre las relaciones entre dos entradas.

covariance()	Covarianza muestral de dos variables.
correlation()	Coeficiente de correlación de Pearson y Spearman.
linear_regression()	Pendiente e intersección para regresión lineal simple.

Detalles de las funciones

Nota: Las funciones no requieren que se ordenen los datos que se les proporcionan. Sin embargo, para facilitar la lectura, la mayoría de los ejemplos muestran secuencias ordenadas.

statistics.mean(data)

Retorna la media aritmética muestral de data, que puede ser una secuencia o un iterable.

La media aritmética es la suma de los valores dividida entre el número de observaciones. Es comúnmente denominada «promedio», aunque hay muchas formas de definir el promedio matemáticamente. Es una medida de tendencia central de los datos.

Se lanza una excepción StatisticsError si data está vacío.

Algunos ejemplos de uso:

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

Nota

La media se ve muy afectada por los outliers y no es necesariamente un ejemplo típico de los puntos de datos. Para una medida más robusta, aunque menos eficiente, de la tendencia central, véase median().

La media muestral proporciona una estimación no sesgada de la media real de la población. Por lo tanto, al calcular el promedio de todas las muestras posibles, mean(sample) converge con el promedio real de toda la población. Si data representa a una población completa, en lugar de a una muestra, entonces mean(data) equivale a calcular la media poblacional verdadera μ.

statistics.fmean(data, weights=None)

Convierte los valores de data a flotantes y calcula la media aritmética.

Esta función se ejecuta más rápido que mean() y siempre retorna un float. data puede ser una secuencia o un iterable. Si el conjunto de datos de entrada está vacío, se lanza una excepción StatisticsError.

>>> fmean([3.5, 4.0, 5.25])
4.25

La ponderación es opcional. Por ejemplo, un profesor asigna una nota a un curso ponderando las pruebas en un 20%, los deberes en un 20%, un examen parcial en un 30% y un examen final en un 30%:

>>> grades = [85, 92, 83, 91]
>>> weights = [0.20, 0.20, 0.30, 0.30]
>>> fmean(grades, weights)
87.6

Si se proporciona weights, debe tener la misma longitud que los data o se producirá un ValueError.

Added in version 3.8.

Distinto en la versión 3.11: Soporte añadido a weights.

statistics.geometric_mean(data)

Convierte los valores de data a flotantes y calcula la media geométrica.

La media geométrica indica la tendencia central o valor típico de data utilizando el producto de los valores (en oposición a la media aritmética, que utiliza su suma).

Lanza una excepción StatisticsError si el conjunto de datos de entrada está vacío, o si contiene un cero o un valor negativo. data puede ser una secuencia o un iterable.

No se toman medidas especiales para garantizar que el resultado sea completamente preciso. (Sin embargo, esto puede cambiar en una versión futura.)

>>> round(geometric_mean([54, 24, 36]), 1)
36.0

Added in version 3.8.

statistics.harmonic_mean(data, weights=None)

Return the harmonic mean of data, a sequence or iterable of real-valued numbers. If weights is omitted or None, then equal weighting is assumed.

La media armónica es recíproco de la mean() aritmética de los recíprocos de los datos. Por ejemplo, la media armónica de tres valores a, b and c es equivalente a 3/(1/a + 1/b + 1/c). Si alguno de los valores es cero, el resultado va a ser cero.

La media armónica es un tipo de promedio, una medida de la tendencia central de los datos. Generalmente es adecuada para calcular promedios de tasas o fracciones, por ejemplo, velocidades.

Supongamos que un automóvil viaja 10 km a 40 km/h, luego otros 10 km a 60 km/h. ¿Cuál es su velocidad media?

>>> harmonic_mean([40, 60])
48.0

Supongamos que un un automóvil viaja 5 km a 40 km/h, y cuando el tráfico se despeja, acelera a 60 km/h durante los 30 km restantes del viaje. ¿Cuál es su velocidad media?

>>> harmonic_mean([40, 60], weights=[5, 30])
56.0

Una excepción StatisticsError es lanzada si data está vacío, algún elemento es menor que cero, o si la suma ponderada no es positiva.

El algoritmo actual tiene una salida anticipada cuando encuentra un cero en la entrada. Esto significa que no se comprueba la validez de las entradas posteriores al cero. (Este comportamiento puede cambiar en el futuro.)

Added in version 3.6.

Distinto en la versión 3.10: Soporte añadido a weights.

statistics.median(data)

Retorna la mediana (valor central) de los datos numéricos, utilizando el método clásico de «media de los dos del medio». Si data está vacío, se lanza una excepción StatisticsError. data puede ser una secuencia o un iterable.

La mediana es una medida de tendencia central robusta y es menos sensible a la presencia de valores atípicos que la media. Cuando el número de casos es impar, se retorna el valor central:

>>> median([1, 3, 5])
3

Cuando el número de observaciones es par, la mediana se interpola calculando el promedio de los dos valores centrales:

>>> median([1, 3, 5, 7])
4.0

Este enfoque es adecuado para datos discretos, siempre que se acepte que la mediana no es necesariamente parte de las observaciones.

Si los datos son ordinales (se pueden ordenar) pero no numéricos (no se pueden sumar), considera usar median_low() o median_high() en su lugar.

statistics.median_low(data)

Retorna la mediana baja de los datos numéricos. Se lanza una excepción StatisticsError si data está vacío. data puede ser una secuencia o un iterable.

La mediana baja es siempre un valor presente en el conjunto de datos. Cuando el número de casos es impar, se retorna el valor central. Cuando el número de casos es par, se retorna el menor de los dos valores centrales.

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

Utiliza la mediana baja cuando tus datos sean discretos y prefieras que la mediana sea un valor representado en tus observaciones, en lugar de ser el resultado de una interpolación.

statistics.median_high(data)

Retorna la mediana alta de los datos. Lanza una excepción StatisticsError si data está vacío. data puede ser una secuencia o un iterable.

La mediana alta es siempre un valor presente en el conjunto de datos. Cuando el número de casos es impar, se retorna el valor central. Cuando el número de casos es par, se retorna el mayor de los dos valores centrales.

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

Utiliza la mediana alta cuando tus datos sean discretos y prefieras que la mediana sea un valor representado en tus observaciones, en lugar de ser el resultado de una interpolación.

statistics.median_grouped(data, interval=1.0)

Estimates the median for numeric data that has been grouped or binned around the midpoints of consecutive, fixed-width intervals.

The data can be any iterable of numeric data with each value being exactly the midpoint of a bin. At least one value must be present.

The interval is the width of each bin.

For example, demographic information may have been summarized into consecutive ten-year age groups with each group being represented by the 5-year midpoints of the intervals:

>>> from collections import Counter
>>> demographics = Counter({
...    25: 172,   # 20 to 30 years old
...    35: 484,   # 30 to 40 years old
...    45: 387,   # 40 to 50 years old
...    55:  22,   # 50 to 60 years old
...    65:   6,   # 60 to 70 years old
... })
...

The 50th percentile (median) is the 536th person out of the 1071 member cohort. That person is in the 30 to 40 year old age group.

The regular median() function would assume that everyone in the tricenarian age group was exactly 35 years old. A more tenable assumption is that the 484 members of that age group are evenly distributed between 30 and 40. For that, we use median_grouped():

>>> data = list(demographics.elements())
>>> median(data)
35
>>> round(median_grouped(data, interval=10), 1)
37.5

The caller is responsible for making sure the data points are separated by exact multiples of interval. This is essential for getting a correct result. The function does not check this precondition.

Inputs may be any numeric type that can be coerced to a float during the interpolation step.

statistics.mode(data)

Retorna el valor más común del conjunto de datos discretos o nominales data.La moda (cuando existe) es el valor más representativo y sirve como medida de tendencia central.

Si hay varias modas con la misma frecuencia, retorna la primera encontrada en data. Si deseas la menor o la mayor de ellas, usa min(multimode(data)) o max(multimode(data)). Se lanza una excepción StatisticsError si la entrada data está vacía.

mode asume que los datos de entrada son discretos y retorna un solo valor. Esta es la definición habitual de la moda que se enseña en las escuelas:

>>> mode([1, 1, 2, 3, 3, 3, 3, 4])
3

La moda tiene la particularidad de ser la única estadística de este módulo que se puede calcular sobre datos nominales (no numéricos):

>>> mode(["red", "blue", "blue", "red", "green", "red", "red"])
'red'

Only hashable inputs are supported. To handle type set, consider casting to frozenset. To handle type list, consider casting to tuple. For mixed or nested inputs, consider using this slower quadratic algorithm that only depends on equality tests: max(data, key=data.count).

Distinto en la versión 3.8: Ahora maneja conjuntos de datos multimodales, retornando la primera moda encontrada. Anteriormente, se lanzaba una excepción StatisticsError cuando se daba esta situación.

statistics.multimode(data)

Retorna una lista de los valores más frecuentes en el orden en que aparecen en data. Retornará varios resultados en el caso de que existan varias modas, o una lista vacía si data está vacío:

>>> multimode('aabbbbccddddeeffffgg')
['b', 'd', 'f']
>>> multimode('')
[]

Added in version 3.8.

statistics.pstdev(data, mu=None)

Retorna la desviación típica poblacional (la raíz cuadrada de la varianza poblacional). Consultar pvariance() para los argumentos y otros detalles.

>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
0.986893273527251

statistics.pvariance(data, mu=None)

Retorna la varianza poblacional de data, que debe ser una secuencia no vacía o un iterable de números reales. La varianza, o momento de segundo orden respecto a la media, es una medida de la variabilidad (o dispersión) de los datos. Una alta varianza indica una amplia dispersión de valores; una varianza baja indica que los valores están agrupados alrededor de la media.

If the optional second argument mu is given, it should be the population mean of the data. It can also be used to compute the second moment around a point that is not the mean. If it is missing or None (the default), the arithmetic mean is automatically calculated.

Utiliza esta función para calcular la varianza de toda la población. Para estimar la varianza de una muestra, la función variance() suele ser una opción mejor.

Lanza una excepción StatisticsError si data está vacío.

Ejemplos:

>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>> pvariance(data)
1.25

Si ya has calculado la media de tus datos, puedes pasarla como segundo argumento opcional mu para evitar que se tenga que volver a calcular:

>>> mu = mean(data)
>>> pvariance(data, mu)
1.25

Se admiten decimales (Decimal) y fracciones (Fraction):

>>> from decimal import Decimal as D
>>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('24.815')

>>> from fractions import Fraction as F
>>> pvariance([F(1, 4), F(5, 4), F(1, 2)])
Fraction(13, 72)

Nota

Esta función retorna la varianza poblacional σ² cuando se aplica a toda la población. Si se aplica solo a una muestra, el resultado es la varianza muestral s², conocida también como varianza con N grados de libertad.

Si se conoce de antemano la verdadera media poblacional μ, se puede usar esta función para calcular la varianza muestral, pasando la media poblacional conocida como segundo argumento. Suponiendo que las observaciones provienen de una selección aleatoria uniforme de la población, el resultado será una estimación no sesgada de la varianza poblacional.

statistics.stdev(data, xbar=None)

Retorna la desviación típica muestral (la raíz cuadrada de la varianza muestral). Consultar variance() para los argumentos y otros detalles.

>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
1.0810874155219827

statistics.variance(data, xbar=None)

Retorna la varianza muestral de data, que debe ser un iterable de al menos dos números reales. La varianza, o momento de segundo orden respecto a la media, es una medida de la variabilidad (difusión o dispersión) de los datos. Una alta varianza indica que los datos están dispersos; una baja varianza indica que los datos están agrupados estrechamente alrededor de la media.

If the optional second argument xbar is given, it should be the sample mean of data. If it is missing or None (the default), the mean is automatically calculated.

Utiliza esta función cuando tus datos sean una muestra de una población. Para calcular la varianza de toda la población, consulta pvariance().

Lanza una excepción StatisticsError si data tiene menos de dos valores.

Ejemplos:

>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> variance(data)
1.3720238095238095

If you have already calculated the sample mean of your data, you can pass it as the optional second argument xbar to avoid recalculation:

>>> m = mean(data)
>>> variance(data, m)
1.3720238095238095

Esta función no comprueba si el valor pasado al argumento xbar corresponde al promedio. El uso de valores arbitrarios para xbar produce resultados imposibles o incorrectos.

La función maneja decimales (Decimal) y fracciones (Fraction):

>>> from decimal import Decimal as D
>>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('31.01875')

>>> from fractions import Fraction as F
>>> variance([F(1, 6), F(1, 2), F(5, 3)])
Fraction(67, 108)

Nota

Esta es la varianza muestral s² con la corrección de Bessel, también conocida como varianza con N-1 grados de libertad. Suponiendo que las observaciones son representativas de la población (es decir, independientes y distribuidas de forma idéntica), el resultado es una estimación no sesgada de la varianza.

Si conoces de antemano la verdadera media poblacional μ, debes pasarla a pvariance() mediante el parámetro mu para obtener la varianza muestral.

statistics.quantiles(data, *, n=4, method='exclusive')

Divide data en n intervalos continuos equiprobables. Retorna una lista de n - 1 límites que delimitan los intervalos (cuantiles).

Establece n en 4 para obtener los cuartiles (el valor predeterminado), en 10 para obtener los deciles y en 100 para obtener los percentiles (lo que produce 99 valores que separan data en 100 grupos del mismo tamaño). Si n es menor que 1, se lanza una excepción StatisticsError.

data puede ser cualquier iterable que contenga los valores de la muestra. Para que los resultados sean significativos, el número de observaciones en la muestra data debe ser mayor que n. Si no hay al menos dos observaciones se lanza una excepción StatisticsError.

Los límites de los intervalos se interpolan linealmente a partir de los dos valores más cercanos de la muestra. Por ejemplo, si un límite es un tercio de la distancia entre los valores 100 y 112 de la muestra, el límite será 104.

El argumento method indica el método que se utilizará para calcular los cuantiles y se puede modificar para especificar si se deben incluir o excluir valores de data extremos, altos y bajos, de la población.

El valor predeterminado para method es «exclusive» y es aplicable a los datos muestreados de una población que puede tener valores más extremos que los encontrados en las muestras. La proporción de la población que se encuentra por debajo del i-ésimo valor de m valores ordenados se calcula mediante la fórmula i / (m + 1). Por ejemplo, asumiendo que hay 9 valores en la muestra, este método los ordena y los asocia con los siguientes percentiles: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%.

Si se usa «inclusive» como valor para el parámetro method, se asume que los datos corresponden a una población completa o que los valores extremos de la población están representados en la muestra. El valor mínimo de data se considera entonces como percentil 0 y el máximo como percentil 100. La proporción de la población que se encuentra por debajo del i-ésimo valor de m valores ordenados se calcula mediante la fórmula (i - 1) / (m - 1). Suponiendo que tenemos 11 valores en la muestra, este método los ordena y los asocia con los siguientes percentiles: 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80 %, 90%, 100%.

# Decile cut points for empirically sampled data
>>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
...         100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
...         106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
...         111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
...         103, 107, 101, 81, 109, 104]
>>> [round(q, 1) for q in quantiles(data, n=10)]
[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

Added in version 3.8.

statistics.covariance(x, y, /)

Retorna la covarianza de muestra de dos entradas x y y. La covarianza es una medida de la variabilidad conjunta de dos entradas.

Ambas entradas deben ser del mismo largo (no menor a dos), de lo contrario se lanza StatisticsError.

Ejemplos:

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> covariance(x, y)
0.75
>>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> covariance(x, z)
-7.5
>>> covariance(z, x)
-7.5

Added in version 3.10.

statistics.correlation(x, y, /, *, method='linear')

Retorna el coeficiente de correlación de Pearson para dos entradas. El coeficiente de correlación de Pearson r toma valores entre -1 y +1. Mide la fuerza y dirección de la relación lineal.

Si method es «ranked», calcula El coeficiente de correlación de Spearman para dos entradas. Los datos se sustituyen por rangos. Los empates se promedian para que valores iguales reciban el mismo rango. El coeficiente resultante mide la fuerza de una relación monótona.

El coeficiente de correlación de Spearman es apropiado para datos ordinales o para datos continuos que no cumplen el requisito de proporción lineal para el coeficiente de correlación de Pearson.

Ambas entradas deben ser del mismo largo (no menor a dos), y no necesitan ser constantes, de lo contrario se lanza StatisticsError.

Ejemplo con “Leyes de Kepler sobre el movimiento planetario <https://es.wikipedia.org/wiki/Leyes_de_Kepler’_:

>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and  Neptune
>>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190]    # days
>>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km

>>> # Show that a perfect monotonic relationship exists
>>> correlation(orbital_period, dist_from_sun, method='ranked')
1.0

>>> # Observe that a linear relationship is imperfect
>>> round(correlation(orbital_period, dist_from_sun), 4)
0.9882

>>> # Demonstrate Kepler's third law: There is a linear correlation
>>> # between the square of the orbital period and the cube of the
>>> # distance from the sun.
>>> period_squared = [p * p for p in orbital_period]
>>> dist_cubed = [d * d * d for d in dist_from_sun]
>>> round(correlation(period_squared, dist_cubed), 4)
1.0

Added in version 3.10.

Distinto en la versión 3.12: Soporte añadido para el coeficiente de correlación de Spearman.

statistics.linear_regression(x, y, /, *, proportional=False)

Retorna la pendiente e intersección de los parámetros de una regresión lineal simple estimados usando mínimos cuadrados ordinarios. La regresión lineal simple describe la relación entre la variable independiente x y la variable dependiente y en términos de esta función lineal:

y = slope * x + intercept + noise

donde slope e intercept son los parámetros de regresión que son estimados, y noise representa la variabilidad de los datos que no fue explicado por la regresión lineal (es igual a la diferencia entre los valores predichos y reales de la variable dependiente).

Ambas entradas deben ser del mismo largo (no menor a dos), y la variable independiente x no puede ser constante, de lo contrario se lanza StatisticsError.

Por ejemplo, podemos usar las fechas de lanzamiento de las películas de Monty Python para predecir el número acumulativo de películas de Monty Python que se habría producido en 2019 asumiendo que hubiesen mantenido el ritmo:

>>> year = [1971, 1975, 1979, 1982, 1983]
>>> films_total = [1, 2, 3, 4, 5]
>>> slope, intercept = linear_regression(year, films_total)
>>> round(slope * 2019 + intercept)
16

Si proportional es verdadero, se supone que la variable independiente x y la variable dependiente y son directamente proporcionales. Los datos se ajustan a una recta que pasa por el origen. Como la intercept siempre será 0,0, la función lineal subyacente se simplifica a:

y = slope * x + noise

Continuing the example from correlation(), we look to see how well a model based on major planets can predict the orbital distances for dwarf planets:

>>> model = linear_regression(period_squared, dist_cubed, proportional=True)
>>> slope = model.slope

>>> # Dwarf planets:   Pluto,  Eris,    Makemake, Haumea, Ceres
>>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680]  # days
>>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods]
>>> list(map(round, predicted_dist))
[5912, 10166, 6806, 6459, 414]

>>> [5_906, 10_152, 6_796, 6_450, 414]  # actual distance in million km
[5906, 10152, 6796, 6450, 414]

Added in version 3.10.

Distinto en la versión 3.11: Soporte añadido a proportional.

Excepciones

Se define una sola excepción:

exception statistics.StatisticsError

Subclase de ValueError para excepciones relacionadas con la estadística.

Objetos NormalDist

NormalDist es una herramienta para crear y manipular distribuciones normales de una variable aleatoria. Esta clase gestiona la desviación típica y la media de un conjunto de observaciones como una sola entidad.

Las distribuciones normales surgen del Teorema del límite central y tienen una amplia gama de aplicaciones en estadística.

class statistics.NormalDist(mu=0.0, sigma=1.0)

Retorna un nuevo objeto NormalDist donde mu representa la media aritmética y sigma representa la desviación típica.

Se lanza una excepción StatisticsError si sigma es negativo.

mean

Una propiedad de solo lectura para la media aritmética de una distribución normal.

median

Una propiedad de solo lectura para la mediana de una distribución normal.

mode

Una propiedad de solo lectura para la moda de una distribución normal.

stdev

Una propiedad de solo lectura para la desviación típica de una distribución normal.

variance

Una propiedad de solo lectura para la varianza de una distribución normal. Es igual al cuadrado de la desviación típica.

classmethod from_samples(data)

Crea una instancia de distribución normal con los parámetros mu y sigma estimados a partir de data usando fmean() y stdev().

data puede ser cualquier iterable de valores que se puedan convertir al tipo float. Se lanza una excepción StatisticsError si data no contiene al menos dos elementos, esto se debe a que se necesita al menos un punto para estimar un valor central y al menos dos puntos para estimar la dispersión.

samples(n, *, seed=None)

Genera n muestras aleatorias para una media y una desviación típica proporcionadas. Retorna un objeto list de valores float.

Si se proporciona seed, su valor se usa para inicializar una nueva instancia del generador de números aleatorios subyacente. Esto permite producir resultados reproducibles incluso en un contexto de paralelismo con múltiples hilos.

pdf(x)

Haciendo uso de una función de densidad de probabilidad (FPD o PDF en inglés), calcula la verosimilitud relativa de que una variable aleatoria X caiga en una región cercana al valor x proporcionado. Matemáticamente, esto corresponde al límite de la razón P(x <= X < x+dx) / dx cuando dx tiende a cero.

La verosimilitud relativa se calcula como la probabilidad de que una observación pertenezca a un intervalo estrecho dividida entre el ancho del intervalo (de ahí el término «densidad»). Como la verosimilitud es relativa a los otros puntos, su valor puede ser mayor que 1.0.

cdf(x)

Usando una función de distribución acumulada (FDA, CDF en inglés), calcula la probabilidad de que una variable aleatoria X sea menor o igual que x. Matemáticamente, se escribe P(X <= x).

inv_cdf(p)

Calcula la función de distribución acumulada inversa, también conocida como función cuantil o función punto porcentual. Matemáticamente, se escribe x : P(X <= x) = p.

Calcula el valor x de la variable aleatoria X tal que la probabilidad de que la variable sea menor o igual a este valor es igual a la probabilidad p dada.

overlap(other)

Mide la concordancia entre dos distribuciones de probabilidad normales. Retorna un valor entre 0.0 y 1.0 que indica el área de superposición de dos funciones de densidad de probabilidad.

quantiles(n=4)

Divide la distribución normal en n intervalos continuos equiprobables. Retorna una lista de (n - 1) cuantiles que separan los intervalos.

Establece n en 4 para obtener los cuartiles (el valor predeterminado), en 10 para obtener los deciles y en 100 para obtener los percentiles (lo que produce 99 límites que separan los datos en 100 grupos del mismo tamaño).

zscore(x)

Computa el Standard Score describiendo x en términos de los números de desviaciones estándar sobre o bajo la media de una distribución normal: (x - mean) / stdev.

Added in version 3.9.

Las instancias de la clase NormalDist soportan la suma, resta, multiplicación y división por una constante. Estas operaciones se pueden utilizar para traducir o escalar, por ejemplo:

>>> temperature_february = NormalDist(5, 2.5)             # Celsius
>>> temperature_february * (9/5) + 32                     # Fahrenheit
NormalDist(mu=41.0, sigma=4.5)

No se admite la división de una constante entre una instancia de NormalDist debido a que el resultado no sería una distribución normal.

Dado que las distribuciones normales se derivan de las propiedades aditivas de variables independientes, es posible sumar o restar dos variables independientes con distribución normal representadas por instancias de NormalDist. Por ejemplo :

>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5])
>>> drug_effects = NormalDist(0.4, 0.15)
>>> combined = birth_weights + drug_effects
>>> round(combined.mean, 1)
3.1
>>> round(combined.stdev, 1)
0.5

Added in version 3.8.

Examples and Recipes

Problemas de probabilidad clásicos

NormalDist permite resolver fácilmente problemas probabilísticos clásicos.

Por ejemplo, sabiendo que los datos históricos de los exámenes SAT siguen una distribución normal con una media de 1060 y una desviación típica de 195, determinar el porcentaje de estudiantes con puntuaciones entre 1100 y 1200, redondeado al número entero más cercano:

>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4

Determinar los cuartiles y deciles de las puntuaciones del SAT:

>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]

Entradas de Monte Carlo para simulaciones

To estimate the distribution for a model that isn’t easy to solve analytically, NormalDist can generate input samples for a Monte Carlo simulation:

>>> def model(x, y, z):
...     return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))       
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]

Aproximación de la distribución binomial

Las distribuciones normales se pueden utilizar para aproximar distribuciones binomiales cuando el tamaño de la muestra es grande y la probabilidad de un ensayo exitoso es cercana al 50%.

Por ejemplo, 750 personas asisten a una conferencia sobre código abierto y se dispone de dos salas con capacidad para 500 personas cada una. En la primera sala hay una charla sobre Python, en la otra una sobre Ruby. En conferencias pasadas, el 65% de las personas prefirieron escuchar las charlas sobre Python. Suponiendo que las preferencias de la población no hayan cambiado, ¿cuál es la probabilidad de que la sala de Python permanezca por debajo de su capacidad máxima?

>>> n = 750             # Sample size
>>> p = 0.65            # Preference for Python
>>> q = 1.0 - p         # Preference for Ruby
>>> k = 500             # Room capacity

>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402

>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402

>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406

Clasificador bayesiano ingenuo

Las distribuciones normales a menudo están involucradas en el aprendizaje automático.

Wikipedia detalla un buen ejemplo de un clasificador bayesiano ingenuo. El reto consiste en predecir el género de una persona a partir de características físicas que siguen una distribución normal, como la altura, el peso y el tamaño del pie.

Disponemos de un conjunto de datos de entrenamiento que contiene las medidas de ocho personas. Se supone que estas medidas siguen una distribución normal, por lo que podemos sintetizar los datos usando NormalDist:

>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])

A continuación, nos encontramos con un nuevo individuo del que conocemos las medidas de sus características pero no su género:

>>> ht = 6.0        # height
>>> wt = 130        # weight
>>> fs = 8          # foot size

Partiendo de una probabilidad a priori del 50% de ser hombre o mujer, calculamos la probabilidad a posteriori como el producto de la probabilidad a priori y la verosimilitud de las diferentes medidas dado el género:

>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
...                   weight_male.pdf(wt) * foot_size_male.pdf(fs))

>>> posterior_female = (prior_female * height_female.pdf(ht) *
...                     weight_female.pdf(wt) * foot_size_female.pdf(fs))

La predicción final es la que tiene mayor probabilidad a posteriori. Este enfoque se denomina máximo a posteriori o MAP:

>>> 'male' if posterior_male > posterior_female else 'female'
'female'

Estimación de la densidad del núcleo

It is possible to estimate a continuous probability distribution from a fixed number of discrete samples.

The basic idea is to smooth the data using a kernel function such as a normal distribution, triangular distribution, or uniform distribution. The degree of smoothing is controlled by a scaling parameter, h, which is called the bandwidth.

from random import choice, random

def kde_normal(data, h):
    "Create a continuous probability distribution from discrete samples."

    # Smooth the data with a normal distribution kernel scaled by h.
    K_h = NormalDist(0.0, h)

    def pdf(x):
        'Probability density function.  P(x <= X < x+dx) / dx'
        return sum(K_h.pdf(x - x_i) for x_i in data) / len(data)

    def cdf(x):
        'Cumulative distribution function.  P(X <= x)'
        return sum(K_h.cdf(x - x_i) for x_i in data) / len(data)

    def rand():
        'Random selection from the probability distribution.'
        return choice(data) + K_h.inv_cdf(random())

    return pdf, cdf, rand

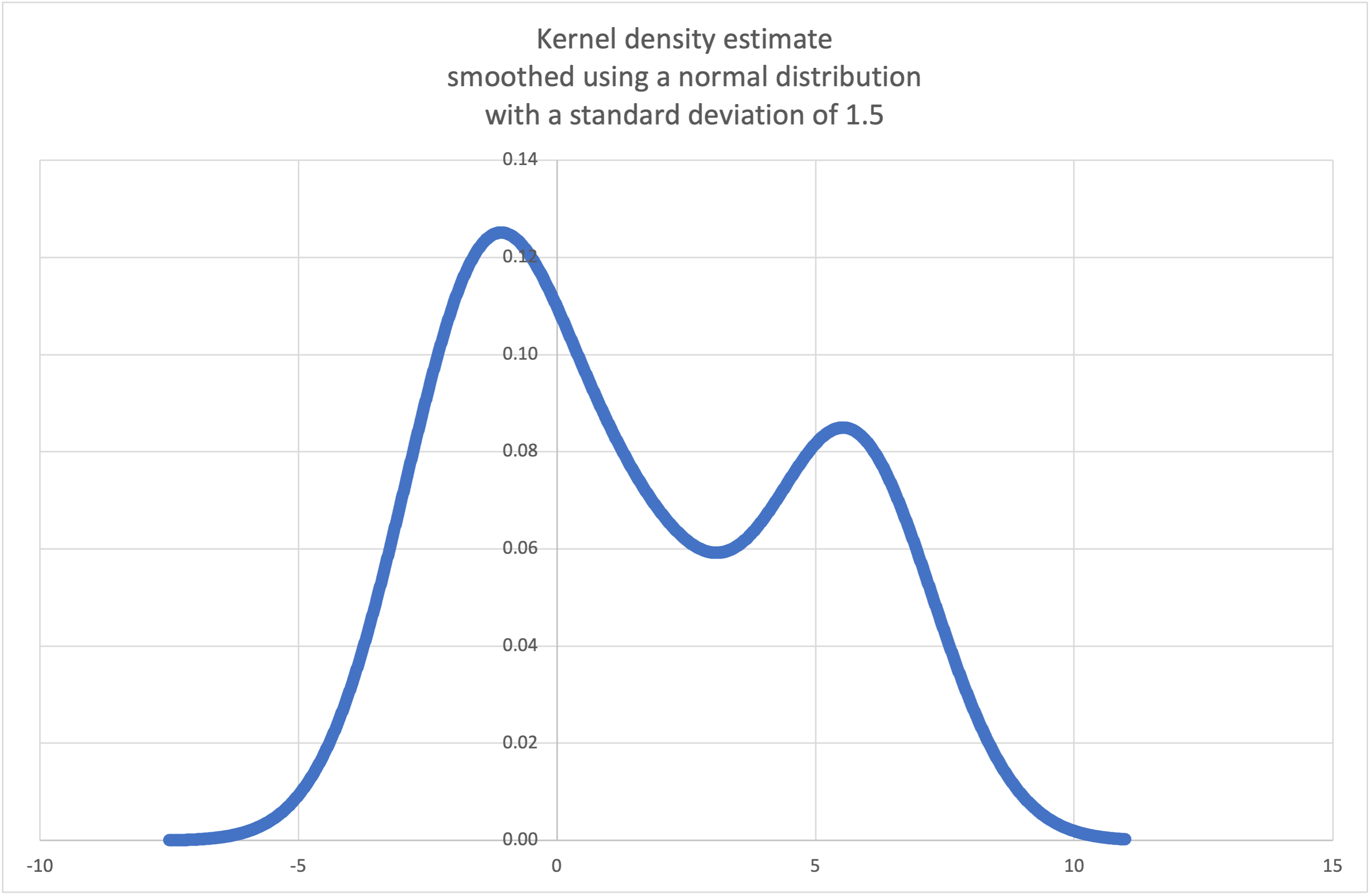
“Wikipedia tiene un ejemplo <https://es.wikipedia.org/wiki/Estimaci%C3%B3n_de_Densidad_de_Kernel#Ejemplo>”_ donde podemos usar la fórmula kde_normal() para generar y trazar una función de densidad de probabilidad estimada a partir de una muestra pequeña:

>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> pdf, cdf, rand = kde_normal(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [pdf(x) for x in xarr]

Los puntos de xarr y yarr pueden utilizarse para hacer una gráfica de la función de densidad de probabilidad:

Resample the data to produce 100 new selections:

>>> new_selections = [rand() for i in range(100)]

Determine the probability of a new selection being below 2.0:

>>> round(cdf(2.0), 4)
0.5794

Add a new sample data point and find the new CDF at 2.0:

>>> sample.append(4.9)
>>> round(cdf(2.0), 4)
0.5005